An Alternative Approach to Nonhydrostatic Modeling, Part III: Nonlinear Mountain Wave Test

Z.I. Janjic¹⁾, J.P. Gerrity, Jr.¹⁾ and S. Nickovic²⁾

As yet another test of the soundness of our nonhydrostatic formulation, we performed a nonlinear mountain wave experiment similar to that of Bubnova et al. (1995). The experimental set-up involves a “bell shaped” hill of 400 m height and 400 m half-width. The initial horizontal wind was set to 4 and the temperature was set to provide a Brunt‑Vaisala stability parameter N approximately equal to . The horizontal grid size was 80 m covering a domain of 16 km. The pressure at the top was set to 340 hPa, and the sea level pressure was set to . The height of the model’s atmosphere was about 8 km. The vertical coordinate used 80 layers of equal mass (constant ) which provides about 100 m vertical spacing on the average. The time step was again . Over the elevated topography, the surface pressure was computed initially using the hypsometric equation and the assigned horizontally homogeneous, thermal profile. However, there were differences in the treatment of the lateral boundary conditions compared to the test by Bubnova et al. (1995). Instead of the Davies-Kallberg relaxation (Davies, 1976), the periodicity was required, and, in addition to that, the Rayleigh damping was applied with the weight proportional to

for .

Here, d is the distance of the grid point from the point located at zero height in the middle of the integration domain in the direction of the x axis. The maximum distance is defined as the distance of the uppermost point at the left boundary from this point. In the semi-circular domain the damping is not applied, while in the rest of the integration domain it operates with the intensity increasing with distance, as described by the formula. In the main test was set to 7000 m, and for the maximum distance, the weight reached the maximum of 0.03. With this arrangement, the Rayleigh damping was applied at the lateral, as well as at the upper boundary. In the tests of Bubnova et al. (1995), this technique was applied only at the upper boundary, starting from rather low 5600 m.

The divergence damping was not used and there was no time filtering of the basic variables. However, the diffusion coefficients along the x and axes were, respectively, 0.001 and 0.0003 for u, 0.010 and 0.0 for T, and 0.0 and 0.0 for w.

The deviation of the horizontal wind from the basic state after 2 hours is shown in Fig. 1 with the contour interval of 0.4 . As in Bubnova et al (1996) figures, the hill is positioned 3.6 km from the left border of the figure, which covers a total width of 11.4 km. The vertical extent of the figure is 7 km. The dashed contours indicate negative values. As can be seen from the figure, the solution is marked by the slanted upward propagation of the perturbation away from the obstacle, as one would expect. The result shown in Fig. 1 is similar to that obtained by Bubnova et al. (1995). However, because the solutions are of finite amplitude and nonlinear, verification against known exact solutions is not possible. The observed differences between the numerical solutions can be explained by different lateral and upper boundary conditions, and different damping parameters and procedures. In the flow regimes considered here, the solutions are very sensitive to both boundary condition specification and damping. This aspect of the problem requires further study that goes beyond the scope of the present research.

Finally, the evolution over the 2 hour forecast period of the momentum flux normalized by its low level value is presented in Fig. 2. The sigma level is on the abscissa, and the flux profiles after, respectively, 1800 s, 3600 s, 5400 s and 7200 s are marked by filled circles, filled diamonds, empty circles and empty diamonds. As pointed out by Bubnova et al. (1995), the profiles oscillate with height, with the values slowly increasing in time. The growth rate, however, appears to be becoming very slow by the end of the forecast period.

_________________________________________________

¹⁾ NCEP/EMC, 5200 Auth Rd., Camp Springs, MD 20746

²⁾ University of Athens, Greece and ICoD, University of Malta, Valetta

e-mail: zavisa.janjic@noaa.gov

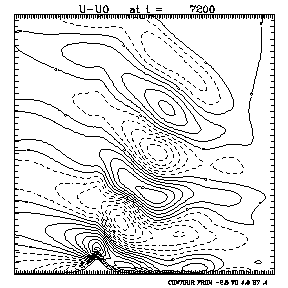
Fig. 1. The deviation of the horizontal wind from its initial uniform value () after 2 hours. The hill is positioned 3.6 km from the left border of the figure, which covers a total width of 11.4 km. The vertical extent of the figure is 7 km. The contour interval is 0.4 and the dashed contours indicate negative values.

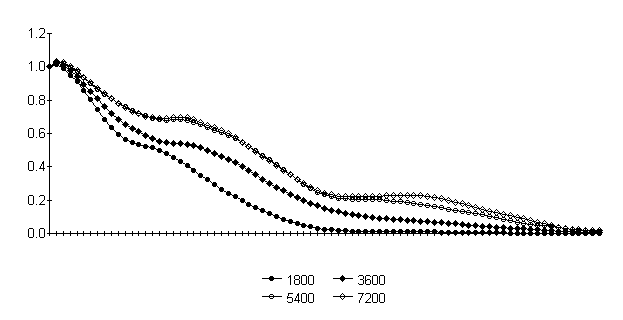
Fig. 2. Evolution over 2 hours of the momentum flux normalized by its low level value. The sigma levels are on the abscissa. The flux profiles after, respectively, 1800 s, 3600 s, 5400 s and 7200 s are marked by filled circles, filled diamonds, empty circles and empty diamonds.

REFERENCES

Bubnova, R., G. Hello, P. Benard and J‑F Geleyn, 1995: Integration of the fully elastic equations cast in the hydrostatic pressure terrain‑following coordinate in the framework of the ARPEGE/Aladin NWP system. Mon. Wea. Rev., 123, 515‑535.

Davies, H.C., 1976: A lateral boundary formulation for multi‑level prediction models. Quart. J. Roy. Meteor. Soc. 102, 405‑418.