Alternative Non-hydrostatic Meso Model Applied to the Wasatch Mountain Wind Storm of 2/24/97

Zavisa Janjic and Geoff DiMego

NCEP/EMC, 5200 Auth Rd., Camp Springs, MD 20746

As previously reported, an alternative approach to the design of a nonhydrostatic NWP model has been proposed by Janjic et al. (1999) which uses hydrostatic pressure (mass) as the vertical coordinate. The basic idea is to split the system of nonhydrostatic equations into two parts: (a) the part that corresponds basically to the hydrostatic system, except for higher order corrections due to the vertical acceleration and (b) the system of equations that allows computation of the corrections appearing in the first system due to the vertical acceleration. The procedure does not require linearization or approximation of any kind.

The nonhydrostatic model designed using this approach represents a natural, evolutionary extension of a hydrostatic model. The nonhydrostatic effects are introduced in a transparent way through an add-on module. This module can be turned on or off depending on resolution, so that the same model can be run in the hydrostatic mode at lower resolution with no extra cost. This feature appears attractive for models designed for a wide range of horizontal resolutions, and in particular for unified global and regional forecasting systems. The proposed concept has been applied within the three-dimensional NCEP Eta model with full physics (e.g., Chen, et al. 1997; Janjic 1979, 1984, 1990, 1994, 1996a,b; Mesinger et al. 1988; Zhao and Carr 1997), and appears to be computationally robust at all resolutions, and efficient for NWP applications. With the current coding, the extra computational effort required due to the nonhydrostatic extension is of the order of 30% of that required by the hydrostatic dynamics, both in terms of computer time and memory.

Testing of the new model has begun with real data cases. One of the first involves the Wasatch Mountain wind storm of 24 February 1997 (McDonald et al. 1998). NCEP was running its Nest-in-the-west at the time which consisted of the 10 km 60 level hydrostatic Meso Eta. This system did NOT predict the wind storm or associated mountain wave very well. The non-hydrostatic Meso model was run at a horizontal resolution (i.e., the shortest distance between points carrying the same variable on the Arakawa E grid) of 8 km with 32 layers in the vertical. In order to improve the accuracy of the pressure gradient force calculation in the sigma mode, a scheme was used that reduces to the technique proposed by Janjic (1977) for the hydrostatic atmosphere (see also, Janjic 1998). The model topography was defined by bilinear interpolation of the 10' U.S. Navy data. After the interpolation, five-point averaging was applied over the land points in order to eliminate the two-grid-interval wave in the terrain height, and thereby prevent the generation of small scale noise by the mountains in the subsequent integration. Some additional smoothing of topography was applied along the lateral boundaries. The integration domain used in the tests was 4 degrees by 4 degrees in the rotated latitude-longitude coordinate system with the coordinate origin located in the center of the domain. The full model physics was applied. The sensitivity of the forecasts was examined with respect to the hydrostatic/nonhydrostatic dynamics and with respect to the mountain representation (step-mountains versus conventional sigma mountains).

The wind storm occurred on February 24 1997 in the Rocky Mountains, along the slopes of the Wasatch Front east of Salt Lake City, Utah. The flow aloft was predominantly easterly across the slope. The differences between the hydrostatic (not shown) and nonhydrostatic forecasts could hardly be noticed by eye. However, the forecasts were sensitive to the mountain representation. Vertical cross sections along the 41 N latitude (the middle of the domain) and extending from 113 W to 111 W in the horizontal and 1000 m to 6500 m in the vertical, are shown in Figure 1 for (top to bottom) 9 hour, 12 hour and 15 hour hour forecast times starting from 00 UTC, February 24 1997. The results obtained using the step-mountain representation are shown on the left hand side, and the results obtained using the usual sigma coordinate mountain representation are presented in the right hand side of the figure. Isolines of potential temperature and the wind vector are presented in the cross sections. The wind components in the vertical plane are scaled by the respective linear dimensions of the part of the vertical plane shown, and the contour interval for the potential temperature is 2 degrees.

As can be seen from the figure, in the sigma mode the model successfully developed strong low-level down-slope winds reaching maximum intensity between 12 UTC and 15 UTC. This agrees reasonably well with observations that showed the strongest wind at 15 UTC (McDonald et al. 1998). An interesting feature, successfully reproduced in the sigma mode forecast, is the rapid decrease of the low level wind speed with increasing distance from the slope. Apparently, the impact of the nonhydrostatic effects was negligible in this case and the difference between the forecasts is due largely to the technique used to represent the mountains.

_______________________________________

e-mail: zavisa.janjic@noaa.gov

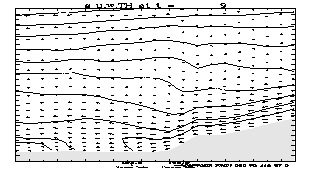
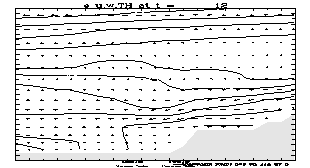
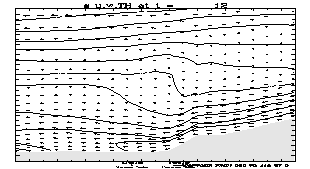
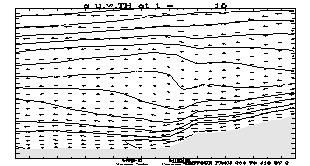
Fig. 1. Cross sections along 41 N extending from 113 W to 111 W, and from 1000 m to 6500 m in the vertical. The 9 hour, 12 hour and 15 hour forecasts (top to bottom) starting from 00 UTC, February 24, 1997 (eta left, sigma right). The potential temperature and wind vector are shown. The contour interval for the potential temperature is 2 degs.

REFERENCES

Chen, F., Z. Janjic and K. Mitchell, 1997: Impact of atmospheric surface-layer parameterization in the new land-surface scheme of the NCEP mesoscale Eta model. Boundary-Layer Meteorology 48, 391-421.

Janjic, Z.I., 1977: Pressure gradient force and advection scheme used for forecasting with steep and small scale topography. Contributions to Atmospheric Physics 50, 186-199.

_____, 1979: Forward-backward scheme modified to prevent two-grid-interval noise and its application in sigma coordinate models. Contributions to Atmospheric Physics 52, 69-84.

_____, 1984: Non-linear advection schemes and energy cascade on semi-staggered grids. Mon. Wea. Rev.,112, 1234-1245.

_____, 1990: The step-mountain coordinate: physical package. Mon.Wea.Rev., 118, 1429-1443.

_____, 1994: The step-mountain eta coordinate model: further developments of the convection, viscous sublayer and turbulence closure schemes. Mon. Wea. Rev.,122, 927-945.

_____, 1996a: The Mellor-Yamada level 2.5 scheme in the NCEP Eta model. Eleventh Conference on Numerical Weather Prediction, Norfolk, VA, 19-23 August 1996; American Meteorological Society, Boston, MA, 333-334.

_____, 1996b: The surface layer in the NCEP Eta model. Eleventh Conference on Numerical Weather Prediction, Norfolk, VA, 19-23 August 1996; American Meteorological Society, Boston, MA, 354-355.

_____, J. P. Gerity, Jr. and S. Nickovic, 1999: An Alternative Approach to Nonhydrostatic Modeling. Submitted to Mon. Wea. Rev.

Janjic, T.Z., 1998: Comments on 'A finite-volume integration method for computing pressure gradient force in general vertical coordinates' by Shian-Jiann Lin (July B, 1997, 123,1749-1762). Quart. J. Roy. Meteor. Soc., 124, 2527-2529.

McDonald, B.E., J.D. Horel, C.J. Stiff and W.J. Steenburgh, 1998: Observations and simulations of three downslope wind events over the northern Wasatch mountains. Preprint 16th Conference on WAF at Phoenix, Amer. Meteor. Soc., Boston, MA, 62-64.

Mesinger, F., Z.I. Janjic, S. Nickovic, D. Gavrilov and D.G. Deaven, 1988: The step-mountain coordinate: model description and performance for cases of Alpine lee cyclogenesis and for a case of an Appalachian redevelopment. Mon. Wea. Rev., 116, 1493-1518.

Zhao, Q., and F.H. Carr, 1997: A prognostic cloud scheme for operational NWP models. Mon. Wea. Rev.,125, 1931-1953.