U.S. DEPARTMENT OF COMMERCE
NATIONAL OCEANIC AND ATMOSPHERIC ADMINISTRATION
NATIONAL WEATHER SERVICE
NATIONAL CENTERS FOR ENVIRONMENTAL PREDICTION
OFFICE NOTE 438
THE NCEP MESO ETA MODEL POST PROCESSOR:A
DOCUMENTATION
HUI-YA CHUANG AND GEOFF MANIKIN
A REVISED VERSION OF OFFICE NOTE 394 BY RUSSELL
TREADON
APRIL 2001
THIS IS AN INTERNALLY REVIEWED MANUSCRIPT,PRIMARILY
INTENDED FOR INFORMAL EXCHANGE OF INFORMATIONAMONG
NCEP STAFF MEMBERS
Table of Contents
-
Introduction
-
The Eta Model
-
The Eta Post Processor - An Overview
-
The Eta Post Processor - Details
4.1 Constant eta and pressure fields
4.2 Sea level pressure
4.2.1 Eta mode
4.2.2 Sigma mode
4.3 Subterranean fields
4.4 Tropopause level data
4.5 FD level fields
4.6 Freezing level data
4.7 Sounding fields
4.8 Surface-based fields
4.9 10m winds and 2m temperatures
4.10 Boundary layer fields
4.11 LFM and NGM look-alike fields
-
Summary
-
References
-
Appendix 1: Using the Eta Post Processor
7.1 Introduction
7.2 Model and post processor source
7.3 Namelist FCSTDATA
7.4 The Control File
7.5 The Template
7.6 Summary
-
Appendix 2: Product generator
1. Introduction
This Office Note describes
the post processor for the National Centers for Environmental Prediction
Eta model. Preliminary to this discussion is a brief review of the Eta
model, emphasizing the model grid and arrangement of variables. A general
overview of the post processor design, usage, and capabilities follows.
Currently 180 unique fields are available from the post processor. The
final section documents these fields and the algorithms used to compute
them. Details for using the post processor in conjunction with the model
are found in Appendix 1. Appendix 2 lists the various NCEP data sets from
which operational Eta model output is available.
The Eta post processor is
not a stagnant piece of code. New output fields, improved algorithms, GRIB
packing, and code optimization are just a few areas in which development
continues. However, it is unlikely that the algorithms discussed in this
Office Note will dramatically change.
2. The Eta Model
Since its introduction by
Phillips (1957) the terrain following sigma coordinate has become the vertical
coordinate of choice in most numerical weather prediction models. A prime
reason for this is simplification of the lower boundary condition. Difficulties
arise in the sigma coordinate when dealing with steep terrain. In such
situations errors in the pressure gradient force computation become significant
because two large terms of opposite must be added (Smagorinsky et al.,
1967). These errors in turn generate advection and diffusion errors. Numerous
methods have been devised to account for this defect of the sigma system.
Mesinger (1984) took a different approach in defining the eta coordinate,
 ,
,
 .
.
In this notation p is pressure
and subscripts rf, s, and t respectively refer to reference pressure, the
model surface, and the model top (pt = 50 mb). The height z is geometric
height. Observe that the sigma coordinate appears as the
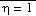
case of the eta coordinate. The reference pressure used in the Eta model
is

, where
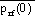
= 1013.25mb, To = 288K,
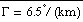
,
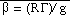
, g=9.8 m/s2, and R = 287.04J/K-kg. In the eta coordinate terrain assumes
a step-like appearance thereby minimizing problems associated with steeply
sloping coordinate surfaces. At the same time the coordinate preserves
the simplified lower boundary condition of a terrain following vertical
coordinate.
The Eta model uses the semi-staggered
Arakawa E grid (Fig. 1). Prognostic variables at mass (H) points are surface
pressure, temperature, and specific humidity. Zonal and meridional wind
components are carried at velocity (V) points. The E grid is mapped to
a rotated latitude-longitude grid which is centered at 50N and 111W for
the current operational Eta with 22 km resolution. Two rotations are involved.
One moves the Greenwich meridian to 111 W. The second shifts the equator
to 50 N. Each row of the E grid lies along a line of constant rotated latitude;
each column lies along a line of constant rotated longitude. In the operational
Eta the shortest distance between like grid points (e.g., d in Fig. 1)
is approximately 22 km at the time of this writing. The large box in Fig.
1 delimits the extent of the computational domain. Prognostic variables
on the outermost rows and columns are specified by a global model forecast
from the previous cycle. The second outermost rows and columns serve to
smoothly blend boundary conditions with values in the computational domain.
The boundaries are one way interactive.
Model terrain is represented
in terms of discrete steps. Each step is centered on a mass point with
a velocity point at each vertex. This is suggested by the dashed box in
Fig. 1. The algorithm creating the steps tends to maximize their heights
(so-called silhouette topography) based on the raw surface elevation data.
Topography over the current operational Eta domain is discretized into
steps from sea level to 3264 meters over the Colorado Rockies.
The current operational Eta
runs with 50 vertical layers. The thickness of the layers varies with greatest
vertical resolution near sea level and around 250mb (to better resolve
jet dynamics). The top of each step coincides exactly with one of the interfaces
between the model's layers. Note that the thickness of the lowest eta layer
above the model terrain is not horizontally homogeneous. This presents
difficulties when posting terrain following fields, which often exhibit
strong horizontal gradients in mountainous regions. Vertical averaging
over several eta layers, sometimes coupled with horizontal smoothing, minimizes
this effect.
Model variables are staggered
vertically as well as horizontally (Fig. 2). Temperature, specific humidity,
and wind components are computed at the midpoint of eta layers. Turbulent
kinetic energy is defined at the interfaces between layers. A no-slip boundary
condition maintains zero wind components along the side of steps. Zero
wind points are circled in Fig. 2.
The model uses a technique
for preventing grid separation (Mesinger 1973, Janjic 1974) in combination
with the split-explict time differencing scheme (Mesinger 1974, Janjic
1979). The fundamental time step for the 22 km operational Eta model is
60 seconds. This is the mass-momentum adjustment time scale. Advection,
physical processes, and cumulus convection march at time steps which are
integral multiples of the fundamental time step. The horizontal advection
algorithm has a built-in strict nonlinear energy cascade control (Janjic,
1984). Vertical advection of moisture is based on the piecewise-linear
method (Carpenter et al, 1989).
Fig. 2. Vertical cross section
through Eta model with N layers. Mass variables such as temperature and
momentum variables such as zonal wind components (T and U respectively)
are defined at the midpoint of each eta layer. Ps is the surface pressure.
The circled wind components along the side of steps are identically zero
as specified by the no-slip boundary used in the model.
The model includes a fairly
sophisticated physics package (Janjic, 1990, 1994) consisting of the Mellor
and Yamada Level 2.5 scheme (Mellor and Yamada 1974, 1982) in the free
atmosphere, the Mellor-Yamada Level 2.0 scheme for the surface layer, and
a viscous sublayer over the oceans (Zilitinkevitch, 1970). Surface processes
are modeled after those of Miyakoda and Sirutis (1984) and Deardorff (1978).
Diffusion uses a second order scheme with the diffusion coefficient depending
on turbulent kinetic energy and deformation of the wind field. Large scale
and parameterized deep and shallow convection are parameterized through
the Betts-Miller-Janjic scheme (1994). The radiation is the NCEP version
of the GFDL radiation scheme with interactive random overlap clouds.
The operational Eta runs from
an analysis based on the regional 3-d variational analysis (3DVAR), with
the first guess for the Eta forecast coming from the Eta-based data assimilation
system (EDAS). The fully cycled EDAS has been used to generate better initial
conditions that require less time for spinup. Boundary conditions for the
model are provided by 6 hour old Aviation model forecasts.
A more complete treatment
of the Eta model can be found in Black et al. (1993) and Black (1994).
Major changes to the Eta model and the Eta Data Assimilation System since
it was implemented in June 1993 are discussed in Rogers et al (1996), Black
et al (1997), Rogers et al (1998), Manikin et al (2000), Rogers et al (2000),
and Rogers et al. (2001). The presentation above was intended to give the
reader a general impression of the Eta model prior to discussing the Eta
post processor below.
3. The Eta Post Processor - An Overview
Various changes have been
made to the Eta post processor since the codes were first written in 1992.
These changes include debugging, adding more posted fields, converting
from 1-D indexing to 2-D indexing, paralleling codes to run on multiple
CPU, and modifying the post to process output from both eta and sigma modes.
The parallelization of the Eta post processor not only reduces the time
it takes to process data but also enables the Eta post to handle domains
with larger dimensions.
The post processor serves
two primary purposes. Foremost, the post processor interpolates forecast
fields horizontally and vertically from the model grid to specified pressure
levels on specified output grids. These posted fields include standard
model output such as geopotential height, temperature, humidity (specific
or relative), vertical motion, and u and v wind components. A second function
of the post processor is to compute special fields from model variables,
such as tropopause level data, FD (flight data) level fields, freezing
level information, and boundary layer fields.
With these purposes in mind
the Eta post processor was designed to be modular, flexible, and relatively
easy to use. A modular approach allows easy introduction of new routines
to compute new output fields or test improved algorithms for currently
posted fields. The user controls posting of fields by editing a control
file. Linking several control files together permits output of data on
multiple grids or files. The structure of the control file was based on
a similar file used with the NGM.
The simplest control file
consists of three primary pieces. First is the header block. Here the user
specifies the format of the posted fields and the output grid. Data is
currently posted in GRIB format. Data may be posted on the staggered E
grid, a filled (i.e., regular) version of this grid, or any grid defined
using standard NCEP grid specifications. All computations involving model
output are done on the staggered model grid. Bilinear interpolation is
used to fill the staggered grid. A second interpolation, which is completed
in the product generator, is required to post data on a regular grid other
than the filled E grid. This interpolation is also bilinear. Those grid
points to which it is not possible to bilinearly interpolate a value to
receive one of two values. A search is made from the outermost rows and
columns of the output grid inward to obtain known values along the edge
of the region to which interpolation was possible. Having identified these
values, the algorithm reverses direction and moves outward along each row
and column. Grid points to which interpolation was not possible are set
equal to the known value along their respective row and column. If after
this operation corner points on the output grid do not have values, they
are assigned the field mean. Depending on the number of output fields requested,
the calculation of interpolation weights can take more CPU time than does
posting the fields. For this reason, interpolation weights may be pre-computed,
saved, and read during post execution. The post retains the ability to
compute these weights internally prior to posting any fields. A character
flag in the header block controls this feature. A second character flag
allows fields on different output grids to be appended to the same output
file using the same or different data formats.
The second section of a control
file lists available fields. By setting integer switches (0=off, 1=on)
the user selects the fields and levels of interest. The current post processor
has 180 unique output fields, some on multiple levels. Room exists for
posting data on up to 60 vertical levels. In posting fields to an output
grid smoothing or filtering of the data may be applied at any of three
steps in the posting process. Fields may be smoothed on the staggered E
grid, filtered on a filled E grid, or filtered on the output grid. Control
of smoothing or filtering is via integer switches. Nonzero integers activate
the smoother or filter with the magnitude of the integer representing the
number of applications (passes) of the selected smoother or filter. The
smoother coded in the post is a fourth order smoother which works directly
on the staggered E grid. Once data is on a regular grid, a 25 point Bleck
filter is available. A nice property of this filter is its fairly sharp
response curve. Repeated applications will remove wavelengths twice the
grid spacing while largely preserving field minima and maxima. Additional
smoothing of posted fields can be realized in the interpolation process
itself. In the current operational post, no smoothing is applied to any
fields.
The last section of each control
file is the end mark. This is a one line statement which tells the post
processor to stop reading the control file and start posting requested
fields. By having an explicit end mark the user only needs to specify the
fields to be posted rather than all 180 available fields with switches
turned off for unwanted fields. The order in which fields are requested
is irrelevant to the post processor. However the order in which fields
are written to the output file is fixed by the code. Figure 3 charts this
ordering. Our discussion of the post processor in Section 4 follows this
flowchart.
Fig. 3. Schematic of flow through post processor.
The Eta post processor is
now also able to process the output of the Eta model forecast in sigma
mode. There are two options in processing sigma output. The first option
interpolates standard model output fields from sigma to pressure coordinates
using traditional bilinear interpolation. The second option uses a cubic
spline fitting method when performing vertical interpolation. The computation
of sea level pressure has been migrated from within the post processor
to within the Eta quilt because the sounding post that runs parallel to
the main post processor needs sea level pressure as input from the restart
files. The sounding post generates the sounding profile. Besides the Shuell
and Mesinger sea level pressure reduction, the addition of processing sigma
restart files using a spline method results in the third option of deducing
sea level pressure in the sigma mode. A logical switch, SPLINE, was put
in the namelist fcstdata.parm which is read in by both the Eta quilt and
the eta post processor. When SPLINE is set to TRUE, the spline fitting
method would be used to perform vertical interpolation, while the bi-linear
interpolation method would be used when SPLINE is set to FALSE. The results
obtained from the two methods do not appear to be very different for the
fields above the ground. However, the underground fields and sea level
pressure field are slightly more smooth when using the spline fitting method.
Additionally, the locations of cyclone centers differ slightly when using
different sea level reduction methods.
4. The Eta Post Processor - Details
The following subsections
discuss fields available from the post and the algorithms used to derive
these fields. Any model user should understand exactly what is represented
by posted model output. Such knowledge allows the user to make more discriminating
decisions when using model output. Further, feedback from users can suggest
alternative algorithms better suited to their needs.
4.1 Constant eta and pressure fields
One can output data on constant
eta or pressure levels. For either option the fields that may be posted
are height, temperature (ambient, potential, and dewpoint), humidity (specific
and relative), moisture convergence, zonal and meridional wind components,
vertical velocity, absolute vorticity, the geostrophic stream function,
cloud water/ice, and turbulent kinetic energy. Pressure may also be posted
on constant eta layers.
Two options exist for posting
eta layer data. Data may be posted from the n-th eta layer. This is simply
a horizontal slice through the three dimensional model grid along the n-th
eta layer. The slice disregards model topography. A second option is to
post fields on the n-th eta layer above the model surface. From the definition
of the eta coordinate it is clear that an eta-based terrain following layer
is generally not a constant mass layer. Despite differences in layer thickness,
examining data in the n-th atmospheric eta layer does have merit. It permits
the user to see what is truly happening in the n-th eta layer above the
model surface and as such represents an eta-based boundary layer perspective.
Additionally, the code can post mass weighted fields in six 30 mb deep
layers stacked above the model surface (see Section 4.10).
The height field on the eta
interfaces is not one of the output variables from the model forecast and
therefore needs to be calculated in the post. The interfaces that overlap
with the eta terrain were specified to be the terrain height. The heights
above the ground on each eta interface are then integrated using temperature
and specific humidity on the eta mid-layers based on the hydrostatic relationship.
The more traditional way of
viewing model output is on constant pressure surfaces. The post processor
currently interpolates fields to thirty-nine isobaric levels (every 25
mb from 50 to 1000 mb). However, the number of isobaric levels to interpolate
fields to can be easily changed by modifying LSM in the parameter statement
of the source code and array SPL(LSM) in the namelist fcstdata.parm. Vertical
interpolation of height is quadratic in log pressure. For temperature,
specific humidity, vertical velocity, horizontal winds, and turbulent kinetic
energy, the vertical interpolation is linear in log pressure. Derived fields
(e.g., dewpoint temperature, relative humidity, absolute vorticity geostrophic
stream function, etc.,) are computed from vertically interpolated base
fields.
The following methods are
used to obtain the fields on the isobaric levels that lie above the model
top (currently 25 mb). Vertical and horizontal wind components above the
model top are specified to be the same as those at the uppermost model
level. For isobaric levels below the lowest model layer, the first atmospheric
eta layer (e.g., the first eta mid-layer above the ground) fields are posted.
Turbulent kinetic energy (TKE) is defined at model interfaces rather than
the midpoint of each layer. At isobaric layers above the model top, the
average TKE over the two uppermost model interfaces is specified. The same
is done for pressure surfaces below the lowest model layer using TKE from
the first and the second interfaces above ground interfaces.
Temperature, humidity, cloud/ice
water, and geopotential heights are treated differently. The temperature
averaged over the two uppermost model layers is used as the temperature
on all the pressure levels above the model top. The specific humidity at
the target level is set so as to maintain the relative humidity averaged
over the two uppermost model layers. The cloud/ice water on the isobaric
levels above the model top is specified as the cloud/ice water on the model
top. Geopotential heights on isobaric surfaces are computed from the temperature
and specific humidity using the hydrostatic equation. The treatment is
the same for isobaric levels below the lowest model layer except that the
averaging is over fields in the second and third model layers above the
surface. This is done because including data from the first atmospheric
layer imposed a strong surface signature on the extrapolated isobaric level
data.
The treatment for the fields
that are underground but above the lowest model layer is very similar to
the treatment for fields below the lowest model layer. Further detail will
be given in section 4.3.
4.2 Sea level pressure
4.2.1 Eta mode
Sea level pressure is one
of the most frequently used fields posted from any operational model. Because
large portions of the Eta Model domain are below the model terrain, some
assumptions must be made to obtain sea level pressure at an underground
grid point. Although there is no one best way to specify the underground
sea level pressure as well as other underground fields, it is desirable
to specify these fields so that they are representable and somewhat smooth.
Although, as mentioned previously, the computation of sea level pressure
is now carried out in the Eta Quilt instead of the Eta Post, the computation
of sea level pressure will still be discussed here for completeness. The
question here is which of a myriad of reduction algorithms to use. Different
reduction algorithms can produce significantly different sea level pressure
fields, given similar input data. The traditional approach is to generate
representative underground temperatures in vertical columns and then integrate
the hydrostatic equation downward. Saucier (1957) devotes several pages
detailing the then current U.S. Weather Bureau reduction scheme. Cram and
Pielke (1989) compare and contrast two reduction procedures using surface
winds and pressure. References for other schemes may be found in their
paper.
Sea level pressure is available
from the Eta model using either of two reduction algorithms. One is based
on a scheme devised by Mesinger (1990). The other is the standard NCEP
reduction algorithm. The methods differ in the technique used to create
fictitious underground temperatures.
The standard reduction algorithm
uses the column approach of vertically extrapolating underground temperatures
from a representative above ground temperature. The algorithm starts with
the hydrostatic equation in the form
 ,
,
Tv = virtual temperature
(approximately given by T(1+ 0.608q); T, the dry air temperature and q,
the specific humidity,
Rd = dry air gas constant,
and
g = gravitational acceleration.
Mean sea level pressure, pmsl,
is computed at mass points using the formula
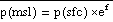
. The function
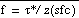
, where
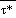
is the average of

at the model surface and
mean sea level. The remaining question is how to determine these
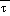
's.
In the NGM
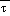
(sfc) and
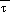
(msl) are first set using a 6.5
K/km lapse rate from the first sigma layer. A similar approach was not
successful in the Eta model due to the discontinuous nature of the step
topography. Virtual temperatures are averaged over eta layers in the first
60 mb above the model surface. The resulting layer mean virtual temperature
field is in turn horizontally smoothed before extrapolating surface and
sea level temperatures.
In both the NGM and Eta,
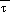
(sfc) and
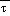
(msl) are subject to the Shuell
correction. Whether this correction is applied depends on the relation
of the extrapolated
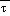
's to a critical value
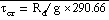
.
The Shuell correction is applied
in two cases:
(1) When only 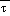 (msl) exceeds
(msl) exceeds 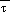 cr, set
cr, set 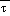 (msl) to
(msl) to 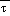 cr,
cr,
(2) When both 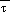 (sfc) and
(sfc) and 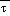 (msl) exceed
(msl) exceed 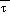 cr, set
cr, set 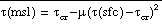 ,
,
where 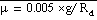 .
.
Once mean sea level pressure
is computed, a consistent 1000 mb height field is obtained using the relation 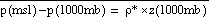 . This simple relationship itself can be used to obtain sea level pressure
given 1000 mb geopotential heights and an assumed mean density. In the
post, the mean density, ?*, is computed from
. This simple relationship itself can be used to obtain sea level pressure
given 1000 mb geopotential heights and an assumed mean density. In the
post, the mean density, ?*, is computed from 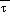 * and p* (the average in log pressure of p(sfc) and p(msl)).
* and p* (the average in log pressure of p(sfc) and p(msl)).
In contrast to the traditional
column approach, the Mesinger scheme uses horizontal interpolation to obtain
underground virtual temperatures. He made an assumption that sea level
pressure should be obtained to maintain the shape of the isobars on surfaces
of constant elevation. Therefore, it is physically more reasonable to create
underground temperatures using atmospheric temperatures surrounding the
mountain rather than extrapolating downward from a single temperature on
the mountain. The step-mountain topography of the Eta model simplifies
coding of this approach. The algorithm starts from the tallest resolved
mountain and steps down through the topography. Virtual temperatures 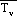 on each step inside the mountain (i.e., underground) are obtained by solving
a Laplace equation:
on each step inside the mountain (i.e., underground) are obtained by solving
a Laplace equation:
 .
.
Atmospheric virtual temperatures
on the same step surrounding the mountain provide consistent, realistic
boundary conditions. The relaxation method is used to smooth the virtual
temperature on all the grid points. However, only the underground virtual
temperature is replaced by the smoothed virtual temperature. In the Eta
Post, (4.2) is solved by applying an eight-point averaging to the virtual
temperature fields on each eta mid-layer:
 ,
,
where A and B are constants,
and ihw and ihe are increments in i directions for the grid points that
are to the west and east of the grid point (i,j). Currently, the eight-point
averaging is applied to the virtual temperature fields 500 times. Once
all underground temperatures have been generated, the hydrostatic equation
(e.g., (4.1)) is integrated downward to obtain sea level pressure. Note
that the thickness dz used to calculate the sea level pressure is not based
on the actual geopotential heights, but the heights of the standard interfaces
which are computed using standard ground level atmospheric temperature
288 K and standard lapse rate 6.5 K/km based on the hydrostatic relationship.
For selected sites the Eta
model posts vertical profile (sounding) data plus several surface fields.
The posting of profile information is not part of the post processor. Sea
level pressures included in the profile data are available only from the
Mesinger scheme in the Eta mode. The standard and Mesinger schemes can
produce markedly different sea level pressure fields given the same input
data. This is especially true in mountainous terrain. The Mesinger scheme
generally produces a smoother analysis, much as one might produce by hand.
4.2.2 Sigma mode
As mentioned previously, there
are two options when processing the Eta model output in sigma mode, SPLINE
and NON-SPLINE, which then produces three different sets of sea level pressure.
Similar to Eta sea level pressure reduction, the first option generates
sea level pressure using both Shuell and Mesinger reduction algorithms.
Recall that the Mesinger sea level reduction involves computation of eight-point
averaging on constant eta levels. Therefore, because the sigma interfaces
are often steep over the mountains, the temperature fields are first interpolated/extrapolated
from sigma to pressure vertical coordinates using the bi-linear interpolation/extrapolation
before the smoothing of the temperature fields is performed. The underground
temperature is then obtained by solving the Laplace equation of temperature
on the constant pressure levels. All the other procedures used to obtain
Mesinger sea level pressure are similar to those in the eta mode.
The procedures for generating
sea level pressure using the second option, the spline fitting method,
are described as follows. First, the spline fitting method is used to interpolate
height fields from sigma to pressure levels. Note that the spline fitting
can only perform interpolation but not extrapolation. Therefore, when the
lowest pressure level falls under the lowest sigma level over a specific
grid point, the bi-linear extrapolation is done to obtain the height at
the lowest pressure level. The sea level pressure at each grid point is
then obtained by finding the pressure level at which height is equal to
zero using the spline fitting method.
4.3 Subterranean fields
The treatment for the underground
fields is very similar to the treatment for fields that are above the surface
but below the lowest model layer as described in section 4.1. The horizontal
wind components on the first atmospheric eta layer above ground are posted
for all the pressure levels below the ground. The underground turbulent
kinetic energy is specified as the average of the first and second layers
above ground. The fictitious underground temperatures on the constant eta
levels generated during deduction of Mesinger sea level pressure were not
used as output temperature for the Eta post. Instead, the underground temperature
calculated during Shuell reduction is currently posted as an underground
temperature on the constant eta levels. Note that there are no underground
fields on the constant sigma levels. The underground temperature on isobaric
levels is then interpolated/extrapolated bilinearly with respect to pressure
using underground temperature on the constant eta levels or specified as
the average of the second and third layers above ground on the constant
sigma levels. Underground specific humidity is adjusted to maintain the
average of the second and third lowest atmospheric eta layer relative humidity.
4.4 Tropopause level data.
The post processor can generate
the following tropopause level fields: pressure, temperature (ambient and
potential), horizontal winds, and vertical wind shear. The greatest difficulty
was coding an algorithm to locate the tropopause above each mass point.
The procedure used in the Eta post processor is based on that in the NGM.
Above each mass point a surface-up search is made for the first occurrence
of three adjacent layers over which the lapse rate is less than a critical
lapse rate. In both the NGM and Eta model the critical lapse rate is 2
K/km. The midpoint (in log pressure) of these two layers is identified
as the tropopause. A lower bound of 500 mb is enforced on the tropopause
pressure. If no two layer lapse rate satisfies the above criteria the model
top is designated the tropopause. Very strong horizontal pressure gradients
result from this algorithm. Horizontal averaging over neighboring grid
points prior to or during the tropopause search might minimize this effect.
To date, this alternative has not been coded. It might be more accurate
to describe the current algorithm as one locating the lowest tropopause
fold above 500 mb.
Linear interpolation in log
pressure from the model layers above and below the tropopause provides
the temperature. Recall that velocity points are staggered with respect
to mass points. Winds at the four velocity points surrounding each mass
point are averaged to provide a mass point wind. These mass point winds
are used in the vertical interpolation to tropopause level. Vertical differencing
between horizontal wind field above and below the tropopause provides an
estimate of vertical wind shear at the tropopause.
4.5 FD level fields.
Flight level temperatures
and winds are posted at six levels, namely 914, 1524, 1829, 2134, 2743,
and 3658 meters above the model surface. At each mass point a surface-up
search is made to locate the model layers bounding the target FD level
height. Linear in log pressure interpolation gives the temperature at the
target height. Again, wind components at the four velocity points surrounding
each mass point are averaged to provide a mass point wind. The wind averaging
is coded so as to not include zero winds in the average. This can happen
in mountainous terrain where the no slip boundary condition of the model
maintains zero winds along the side of steps. Experimentation demonstrated
that the averaging of winds to mass points minimize point maxima or minima
in posted FD level wind fields. The process is repeated for all six flight
level heights.
4.6 Freezing level data.
The post processor computes two types
of freezing level heights and relative humidities at these heights. The
calculation is made at each mass point. To obtain the first type of freezing
level height, a search is made for the two model layers over which the
temperature first falls below 273.16 K when moving up from the model surface.
The second type of freezing level, the highest freezing level, is the last
level whose temperature falls below 273.16 K and the temperature above
it is above 273.16 K when moving from surface up. Vertical interpolation
gives the mean sea level height, temperature, pressure, and specific humidity
at this level. From these fields the freezing level relative humidity is
computed. These fields are used to generate the FOUS 40-43 NWS bulletins
containing six hourly forecasts of freezing level heights and relative
humidities for forecast hours twelve through forty-eight. The surface-up
search algorithm is designed so that posted freezing level heights can
never be below the model terrain. This differs from the LFM algorithm in
which underground heights were possible.
4.7 Sounding fields.
Several lifted indices are
available from the Eta model. All are defined as being the temperature
difference between the temperature of a lifted parcel and the ambient temperature
at 500 mb. The distinction between the indices hinges on which parcel is
lifted. The surface to 500 mb lifted index lifts a parcel from the first
atmospheric eta layer. This lifted index is posted as the traditional LFM
surface to 500 mb lifted index. The thinness of the first atmospheric eta
layer in certain parts of the model domain imparts a strong surface signal
on temperatures and humidities in this layer. In particular strong surface
fluxes can create an unstable first atmospheric layer not representative
of the layers above. The surface to 500 mb lifted index generally indicates
larger areas of instability than other Eta lifted indices.
A second set of lifted indices
are those computed from constant mass or boundary layer fields. The post
can compute mass weighted mean fields in six 30 hPa deep layers stacked
above the model surface. Lifted indices may be computed by lifting a layer
mean parcel from any of these layers. Of six possible lifted indices, the
operational Eta posts that obtained by lifting a parcel from the first
(closest to surface) 30 mb deep layer.
The last lifted index available
from the post processor is similar to the NGM best lifted index. In the
NGM, the best lifted index is the most negative (unstable) lifted index
resulting from lifting parcels in the four lowest sigma layers. The Eta
best lifted index is the most negative lifted index resulting from lifting
parcels in the six constant mass layers.
Two integral, sounding based
fields are available from the Eta post processor: convective available
potential energy (CAPE) and convective inhibition (CINS). As coded in the
post processor, CAPE is the column integrated quantity (Cotton and Anthes
1989)
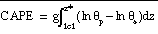
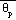
= parcel equivalent potential temperature,
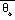
= ambient equivalent potential temperature,
lcl = lifting condensation
level of parcel, and
z* = upper integration
limit.
The parcel to lift is selected
as outlined in Zhang and McFarlane (1991). The algorithm locates the parcel
with the warmest equivalent potential temperature (Bolton, 1980) in the
lowest 70 mb above the model surface. This parcel is lifted from its lifting
condensation level to the equilibrium level, which is defined as the highest
positively buoyant layer in the Eta post. During the lifting process positive
area in each layer is summed as CAPE, negative area as CINS. Typical is
Atkinson's (1981) definition of CAPE

with z* being also the equilibrium
level. Apart from the difference in integration limits this definition
of CAPE and the one coded in the post processor produce qualitatively similar
results. This is easily seen from the power series expansion of

, which shows the integrands to be related.
Posted CAPE values can indicate
a greater potential for convection than may be realized. The search to
determine which parcel to lift starts from the first eta layer above the
surface. As mentioned above, the thinness of this layer over certain parts
of the domain imparts a strong surface signal on temperatures and humidities
in this layer. Instabilities in the first atmospheric eta layer may not
be representative of the layers above. This should be kept in mind when
using CAPE values posted from the operational Eta.
Random overlap clouds are
included in the Eta model radiation package. This code is based on that
in the NCEP global spectral model (Campana and Caplan (1989), Campana et
al. (1990)). Both stratiform and convective clouds are parameterized. Key
variables in the parameterization are relative humidity and convective
precipitation rate. Clouds fall into three categories: low (approximately
640 to 990mb), middle (350 to 640 mb), and high (above 350 mb). Fractional
cloud coverage for stratiform clouds is computed using a quadratic relation
in relative humidity (Slingo, 1980). The operational Eta posts time-averaged
stratiform and convective cloud fractions.
In addition to cloud fractions
the post processor can compute lifting condensation level (LCL) pressure
and height above each mass point. These calculations appear quite sensitive
to the definition of the parcel to lift. Experiments are ongoing to find
an optimal definition of this parcel. Under certain situations the convective
condensation level or level of free convection may be more indicative of
cloud base heights. The modular design of the post processor simplifies
the development of such routines. Currently neither LCL pressure nor heights
are posted from the operational Eta post.
The components of storm motion
and storm-relative helicity are important sounding parameters available
from the Eta model. The actual helicity computation is taken from Davies-Jones
et al. (1990) and is computed over the lowest 3 km, giving a value in m2/s2.
The computation of the storm motion vector (which is used to compute the
helicity value), however, can be done several different ways. Prior to
March 2000, the Eta used the technique described in Davies and Johns (1993)
in which storm motion was defined as 30 degrees to the right of the 0-6
km mean wind at 75% of the speed for mean speeds less than 15 m/s and 20
degrees to the right for speeds greater than 15 m/s. This method was found
to perform very well in `classic' severe weather events in which the vertical
wind shear profile is primarily in the upper-right quadrant of the hodograph.
This method, however, doesn't
produce as desirable results for events with `atypical' vertical wind shear
profiles such as those with weak winds, shifted towards the lower-left
quadrant of the hodograph, or having unusual orientations (such as northwest-flow
events). The Internal Dynamics method (hereafter ID) performs much better
in the unusual shear cases and at least as well as the older method in
the classic cases and is now used in the Eta model.
The ID method assumes that
supercell motion has two components - advection of the storm by a mean
wind and propagation to the right or left of the vertical wind shear due
to internal storm dynamics. The code first determines the 0-6 km mean wind
in the profile. The code next finds the 0 - 0.5 km and 5.5 - 6 km mean
winds to represent the tail and head of the shear vector. The storm motion
vector is then defined as 7.5 m/s to the right of the 0-6 km mean wind
constrained along a line which is both perpendicular to the 0-6 km vertical
wind shear vector and passes through the 0-6 km mean wind. A left-moving
storm would be 7.5 m/s to the left of the 0-6 km mean wind, but since most
Northern Hemispheric supercell storms are right-movers, the left-moving
case is ignored.
4.8 Surface-based fields.
The post processor can output
surface pressure, temperature (ambient, dewpoint, and potential), and humidity
(specific and relative). Surface temperatures and humidities are strictly
surface based and should not be interpreted as being indicative of shelter
level measurements. The model carries running sums of total, grid-scale,
and convective precipitation. The accumulation period for these precipitation
amounts is set in the fcstdata.parm file prior to the model run. Interpolation
of accumulated precipitation amounts from the model grid to other output
grids utilizes an area conserving interpolation scheme. Other surface-based
fields that can be posted include instantaneous and time-averaged incoming
and outgoing radiation, roughness length, friction velocity, and coefficients
proportional to surface momentum and heat fluxes.
Static surface fields may
also be posted. These are the geodetic latitude and longitude of output
grid points, the land-sea mask, the sea ice mask, and arrays from which
three dimensional mass and velocity point masks may be reconstructed. The
land-sea mask defines the land-sea interface in the model. Three dimensional
mass and velocity point masks vertically define model topography. For operational
models the practice is to post model output atop background maps. This
assumes that the model geography matches that of the background map. A
one to one correspondence between the two is obviously not possible. The
same remark holds true in the vertical. These comments should be kept in
mind when interpreting output from any model.
4.9 10-meter winds and 2-meter temperatures.
The post processor computes
anemometer level (10 meter) winds and shelter level (2 meter) temperatures.
Gradients of wind speed and temperature can vary by several orders of magnitude
in the surface-layer. Direct application of the Mellor-Yamada Level 2.0
equations in the surface-layer would require additional model layers to
adequately resolve these gradients. A computationally less expensive approach
is to use a bulk layer parametrization of the surface-layer consistent
with the Mellor-Yamada Level 2.0 model. Lobocki (1993) outlined an approach
to derive surface-layer bulk relationships from higher closure models.
Assuming a horizontally homogenous surface layer at rest the Monin-Obukhov
theory maintains that dimensionless gradients of wind speed and potential
temperature at height z (in the surface-layer) may be represented as a
function of a single variable
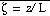
. The length
scale L is the Monin-Obukhov scale. A second important surface-layer parameter
is the flux Richardson number Rf. which quantifies the relative importance
of two production terms in the turbulent kinetic energy equation. Using
the Mellor-Yamada Level 2.0 model, Lobocki derived a fundamental equation
relating internal or surface-layer parameters
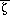
and Rf. with external or bulk characteristics of the surface-layer. Equations
consistent with this fundamental equation relating the wind speed, U, or
potential temperature,
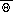
, between two levels,
z1 and z2, in the surface layer are
 .
.
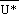
,
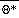
= constant coefficients, and
The functions
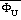
and
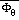
are integrated forms of similarity functions
for dimensionless differences of the quantity U or
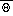
across the layer z1 to z2
Specifically, for S = U or
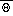
 ,
,
where

is a constant,

, and
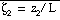
. The function
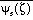
is given by equation (48)
in Lobocki's paper for S = U and (49) for S=
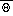
.
When applying these equations
to compute anemometer level winds or shelter level temperatures the height
z2 refers to values in the first eta layer above ground. The height z1
refers to the target level in the surface layer (either 10 or 2 meters).
The dependence of
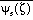
on the Monin-Obukhov height
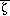
introduces a physically reasonable stability-based variability in computed
anemometer level winds and shelter temperatures. In the absence of strong
synoptic forcing both anemometer level winds and shelter temperatures exhibit
a typical diurnal cycle.
4.10 Boundary layer fields.
The Eta model does not explicitly
forecast fields in a boundary layer. Additionally, the thickness of the
n-th eta layer above the model terrain varies horizontally. The post processor
computes mass-weighted mean fields in six 30 mb deep layers above the model
surface. Note that since the thickness of the n-th eta layer above the
surface varies horizontally the number of layers used in computing mass
weighted means is not horizontally homogenous. Variables that can be posted
from any or all of the six layers are pressure, temperature (ambient, potential,
and dewpoint), humidity (specific and relative), moisture convergence,
horizontal wind components, vertical velocity, and precipitable water.
The precipitable water is that amount obtained by integration over the
constant mass layer. The operational Eta posts all possible boundary layer
fields in the first (lowest) 30 mb layer above the surface. Additionally,
temperature, relative humidity, and winds are posted from the third and
sixth constant mass layers.
Considerable time was spent
developing an algorithm to mimic the behavior of LFM boundary layer winds.
Boundary layer winds from the LFM did not exhibit a diurnal cycle typical
of those from the NGM and Eta model. Rather, LFM boundary layer winds appeared
geostrophic with a superimposed cross isobaric turning towards lower pressure.
To reproduce this effect using the Eta model, the code starts with geostrophic
winds computed from heavily smoothed sea level pressure or 1000 mb heights.
The resulting geostrophic wind components are turned using the classic
Ekman spiral equations (Section 8.5.2 of Haltiner and Williams, 1980).
A rotation parameter controls the amount of the cross contour flow. After
much experimentation a suitable rotation parameter along with appropriate
smoothing was found to produce a wind field very comparable to the LFM
boundary layer winds.
4.11 LFM and NGM look-alike fields.
In addition to posting standard
data on pressure surfaces or deriving other fields from model output, the
post processor generates fields specific to the LFM and NGM using Eta model
output These fields are written to the output file using LFM or NGM labels.
The primary reason for including these look-alike fields was to ensure
compatibility of posted Eta model output with existing graphics and bulletin
generating codes.
The post computes equivalents
to fields in the NGM first (S1=0.98230), third (S3=0.89671), and fifth
(S5=0.78483) sigma layers data as well as layer mean relative humidities
and a layer mean moisture convergence field. Recall the definition of the
sigma coordinate,
 .
.
Given the pressure at the
top of the model and the forecast surface pressure ps, target sigma levels
are converted to pressure equivalents. Vertical interpolation from the
eta layer bounding each target pressure provides an eta-based approximation
to the field on the target sigma level. This calculation is repeated at
each horizontal grid point to obtain eta-based sigma level S1, S3, S5 temperatures,
S1 relative humidity, and S1 u and v wind components. Since surface pressure
is carried at mass points a four point average of the winds surrounding
each mass point is used in computing the S1 u and v wind components. A
check is made to ensure that zero winds are not included in this average.
S3 and S5 relative humidities are layer means over the eta layers mapping
into sigma layers 0.47 to 0.96 and 0.18 to 0.47, respectively.
The FOUS 60-78 NWS bulletins
are generated from the NGM look-alike fields and other posted fields. These
bulletins contain initial condition and six hourly forecasts out to forecast
hour 48 for thirteen parameters at sites over the U.S., Canada, and coastal
waters. Table 1 identifies which Eta fields are used in generating these
bulletins.
Table 1: Posted Eta
model fields used to generate FOUS 60-78 NWS bulletins.
|
|
|
PTT (accumulated precipitation) |
total accumulated precipitation |
Rl (sigma layer 1 relative
humidity) |
NGM look-alike S1 relative
humidity |
R2 (0.47 to 0.96 layer
mean relative humidity) |
NGM look-alike S3 relative
humidity |
R3 (0.18 to 0.47 layer
mean relative humidity) |
NGM look-alike S5 relative
humidity |
VVV (700 mb vertical velocity) |
|
LI (best (NGM four layer)
lifted index) |
Eta best (six layer) lifted
index |
|
|
standard reduction sea
level pressure |
DDFF (sigma layer 1 wind
speed and direction) |
NGM look-alike S1 u and
v winds |
HH (1000-500 mb layer
thickness) |
1000 and 500 mb geopotential
heights |
Tl (sigma layer 1 temperature) |
NGM look-alike S1 temperature |
T3 (sigma layer 3 temperature) |
NGM look-alike S3 temperature |
T5 (sigma layer 5 temperature) |
NGM look-alike S5 temperature |
LFM look-alike fields include
three layer mean relative humidities and a partial column precipitable
water. An approach similar to that used for the NGM is not directly applicable.
The distinction arises due to the vertical structure of the LFM. The approach
taken here was to assume a sigma based vertical coordinate in the LFM and
identify appropriate sigma levels bounding LFM layer mean fields. The sigma
levels used for layer mean relative humidities are 0.33 to l.00, 0.66 to
l.00,and 0.33 to 0.66. For precipitable water the range in sigma is 0.33
to 1.00. Given these sigma bounds the same sigma to eta mapping used for
the NGM fields is applied here.
5. Summary
In this Office Note we have
reviewed the output capabilities of the Eta post processor. Prior to the
post processor description was a brief review of the Eta model with an
emphasis on the horizontal and vertical layout of model variables. Given
this background, we previewed the Eta post processor in general terms.
Key points included the modular design of the post processor and ease of
use. The user controls the post via a control file, specifying not only
which fields to post but also on which grid to post the data and the format
to use. Following this was a field by field description of the algorithms
used to derive posted fields. Users of output from any model should understand
how the output is generated, as this information allows the user to better
use posted model output.
Development continues on the
Eta model and work will continue on the post processor as well. As users
become more familiar with the Eta model it is envisioned that their feedback
will suggest the addition or deletion of routines. Such communication can
play an important but often overlooked role in development.
6. References
Atkinson, B.W., 1981: Meso-scale
Atmospheric Circulations, Academic Press, New York, 495 pp.
Betts, A.K., 1986: A new convective
adjustment scheme. Part I: observational and theoretical basis. Quart.
J. Roy. Meteor Soc., 112, 677-691.
__, and M.J. Miller, 1986:
A new convective adjustment scheme. Part II: single column tests using
GATE wave, BOMFX, and artic air-mass data sets. Quart. J. Roy. Meteor Soc.,
112, 693-709.
Black, T., D. Deaven, and
G. DiMego, 1993: The step-mountain eta coordinate model: 80-km Early version
and objective verifications. NWS Technical Procedures Bulletin No. 412,
NOAA/NWS, 31 pp.
__, 1994: NMC NOTES, The New
NMC Mesoscale Eta Model: Description and Forecast Examples. Wea. Forecasting,
9, 265-278
__, M. Baldwin, K. Brill,
F. Chen, G. DiMego, Z. Janjic, G. Manikin, F. Mesinger, K. Mitchell, E.
Rogers, and Q. Zhao, 1997: Changes to the Eta forecast systems. NWS Technical
Procedures Bulletin No. 441, NOAA/NWS, 10 pp.
Bolton, D., 1980: The computation
of equivalent potential temperature. Mon. Wea. Rev., 108, 1046-1053.
Campana, K.A., and P.M. Caplan,
1989: Diagnosed cloud specifications, Research Highlights of the NMC Development
Division: 1987-1988, 101-111.
__, P.M. Caplan, G.H. White,
S.K. Yang, and H.M. Juang, 1990: Impact of changes to cloud parameterization
on the forecast error of NMC's global model, Preprints Seventh Conference
on Atmospheric Radiation, San Francisco, CA, Amer. Meteor. Soc., J 152-J
158.
Carpenter, R.L., Jr., K.K.
Droegemeier, P.W. Woodward, and C.E. Hane, 1989: Application of the piecewise
parabolic method (PPM) to meteorological modeling. Mon. Wea. Rev., 118,
586-612.
Cotton, W.R., and R.A. Anthes,
1989: Storm and Cloud Dynamics, Academic Press, New York, 880 pp.
Cram, J.M., and R.A. Pielke,
1989: A further comparison of two synoptic surface wind and pressure analysis
methods. Mon. Wea. Rev., 117, 696-706.
Deardorff, J., 1978: Efficient
prediction of ground temperature and moisture with inclusion of a layer
of vegetation. J. Geophys. Res., 83, 1989-1903.
Haltiner, G.J., and R.T. Williams,
1980: Numerical Prediction and Dynamic Meteorology. John Wilely & Sons,
New York, 477 pp.
Janjic, Z. I., 1974: A stable
centered difference scheme free of two-grid-interval noise. Mon. Wea. Rev.,
102, 319-323.
__, 1979: Forward-backward scheme
modified to prevent two-grid-interval noise and its application in sigma
coordinate models. Contrib. Atmos. Phys., 52, 69-84.
__, 1984: Nonlinear advection
schemes and energy cascade on semistaggered grids. Mon. Wea. Rev., 112,
1234-1245.
__, 1990: The step-mountain
coordinate: physical package. Mon. Wea. Rev., 118, 1429-1443. Keyser, D.A.,
1990: NMC Development Division Rotating Random Access Disk Archive - User
Documentation. [Available from NMC, 5200 Auth Road, Washington, D.C., 20233].
Lobocki, L., 1993: A procedure
for the derivation of surface-layer bulk relationships from simplified
second-order closure models. J. Appl. Meteor, 32, 126-138.
Manikin G., M. Baldwin, W. Collins,
J. Gerrity, D. Keyser, Y. Lin, K. Mitchell, and E. Rogers, 2000: Changes
to the NCEP Meso Eta Runs: Extended range, added input, added output, convective
changes. NWS Technical Procedures Bulletin No. 465, NOAA/NWS, 85 pp.
Mellor, G.L., and T. Yamada,
1974: A hierarchy of turbulence closure models for planetary boundary layers.
J. Atmos. Sci., 31,1791-1806.
__, and__, 1982: Development
of a turbulence closure model for geophysical fluid problems. Rev. Geophys.
Space Phys., 20, 851-875.
Mesinger, F., 1973: A method
for construction of second-order accuracy difference schemes permitting
no false two-grid-interval wave in the height field. Tellus, 25, 444-458.
__, 1974: An economical explicit
scheme which inherently prevents the false two-grid-interval wave in forecast
fields. Proc. Symp. on Difference and Spectral Methods for Atmosphere and
Ocean Dynamics Problems, Novosibirsk, Acad. Sci., Novosibirsk, Part II,
18-34.
__, 1984: A blocking technique
for representation of mountains in atmospheric models. Riv. Meteor Aeronautica,
44,195-202.
__, 1990: Horizontal pressure
reduction to sea level. Proc. 21st Conf. for Alpine Meteor, Zurich, Switzerland,
31-35.
Miyakoda, K., and J. Sirutis,
1983: Impact of sub-grid scale parameterizations on monthly forecasts.
Proc. ECMWF Workshop on Convection in Large-Scale Models, ECMWF, Reading,
England, 231-277.
Phillips, N.A., 1957: A coordinate
system having some special advantages for numerical forecasting. J. Meteor.,
14, 297-300.
Rogers, E., T. Black, D. Deaven,
G. DiMego, Q. Zhao, M.Baldwin, and Y. Lin, 1996: Changes to the operational
Early Eta analysis/forecast system and the National Centers for Environmental
Prediction, Wea. Forecasting, 11, 391-413.
__, M. Baldwin, T. Black, K.
Brill, F. Chen, G. DiMego, J. Gerrity, G. Manikin, F. Mesinger, K. Mitchell,
D. Parrish, Q. Zhao, 1997: Changes to the NCEP Operational "Early" Eta
Analysis/ Forecast System. NWS Technical Procedures Bulletin No. 447, NOAA/NWS,
85 pp.
__, T. Black, W. Collins, G.
Manikin, F. Mesinger, D. Parrish and G. DiMego, 2000: Changes to the NCEP
Meso Eta Analysis and Forecast System: Assimilation of satellite radiances
and increase in resolution. NWS Technical Procedures Bulletin No. 473,
NOAA/NWS, 85 pp.
__, M. Ek, Y. Lin, K. Mitchell,
D. Parrish, and G. DiMego, 2001: Changes to the NCEP Meso Eta analysis
and Forecast system: Assimilation of observed precipitation, upgrades to
land-surface physics, modified 3DVAR analysis. NWS Technical Procedures
Bulletin No. 473, NOAA/NWS, 14 pp.
Saucier W.J., 1957: Principles
of Meteorological Analysis, Dover Publications, New York, 438 pp.
Slingo, J.M., 1980: A cloud
parameterization scheme derived from GATE data for use with a numerical
model. Quart J. Roy. Met. Soc., 106, 747-770.
Smagorinsky, J.J., L. Holloway,
Jr., and G.D. Hembree, 1967: Prediction experiments with a general circulation
model, Proc. Inter. Symp. Dynamics Large Scale Atmospheric Processes. Nauka,
Moscow, U.S.S.R., 70-134.
Stackpole, J., 1990: NMC Handbook
[Available from NMC, 5200 Auth Road, Washington, D.C., 20233].
Zhang, G.J., and N.A. McFarlane,
1991: Convective Stabilization in Midlatitudes. Mon. Wea Rev., 119, 1915-1928.
Ziltinkevitch, S.S., 1970: Dynamics
of the planetary boundary layer. Gidrometeorologicheskoe Izdatelystvo,
Leningrad, 292 pp. (in Russian).
7. Appendix 1: Using the Eta Post Processor
7.1 Introduction
In this appendix we discuss
in greater detail how to use the Eta post processor. We assume the reader
knows how to run the Eta model. The peculiarities of any single user application
necessarily limits how specific our treatment can be. It is hoped that
enough information is given to get the reader started using the Eta post
processor.
7.2 Model and post processor source
The source code for the most
current operational eta post processor can be found in /nwprod/sorc/eta_etapost.fd
on the IBM. The source code for the forecast model can be found in /nwprod/sorc/eta_etafcst.fd.
The makefile in each of the two directories is used to compile the post
and forecast codes respectively to generate an executable. Both the post
and forecast source codes have been parallelized to run on multiple processors.
The use of multiple processors has made it possible to run the forecast
and post the model output for domains with larger dimensions which could
not have been accomplished by the serial code due to lack of memory space.
Furthermore, the clock time needed to forecast and post Eta model is greatly
reduced.
7.3 Namelist FCSTDATA
Prior to running the model
the user sets runtime variables in namelist FCSTDATA. These settings affect
both the model and the post processor. A sample FCSTDATA is shown in Fig.7.1.
Fig. 7.1. Sample namelist
FCSTDATA.
The model integration starts
at hour TSTART and runs through hour TEND. If the forecast is part of the
data assimilation cycle, then TCP is set to be equal to TEND and is the
hour at which the restart file restrt03 is generated. When RESTART is set
to true, then the model uses the full restart file as the input initial
condition. Otherwise, the model is initialized with the nfc file (the so-called
"cold-start" restart file). The times (measured in hours) at which to output
forecast files are set in array TSHDE. NMAP is the number of posting times
specified in array TSHDE. The maximum number of posting times is currently
ninety-nine. The only restriction on the output times is that they be between
TSTART and TEND. Array SPL specifies isobaric levels (in Pascals) to which
the post processor can vertically interpolate certain fields. The number
of elements in array SPL is set by parameter LSM in include file parmeta.
The ordering of pressure levels directly maps to level switches in the
post processor control file. This will be covered later when we discuss
the control file in the next section. The variables NPHS and NCNVC represent
how often model surface processes and cumulus convection are executed in
terms of number of model time steps. The frequencies in hours at which
short and long wave radiative processes are set by NRADSH and NRADLH. The
variable NTDDMP specifies how often (in hours) the divergence damping process
is called. Through variables TPREC, THEAT, TCLOD, TRDSW, TRDLW, and TSRFC,
the user specifies the accumulation period (in hours) for accumulation
arrays. Note that the accumulation periods operate independently of the
posting times set in TSHDE. They define the frequency at which accumulated
quantities are reset to zero:
TRDSW = Short wave
radiation
TRDLW = Long wave
radiation
TSRFC = Surface parameters
7.4 The Control File
The user interacts with the
post processor through a control file which has a setup similar to the
one used with the NGM. By editing the control file the user selects which
fields to post, to which grid to post the fields, and in what format to
output the fields. If fields are to be posted to a grid other than the
model grid, interpolation weights may be computed beforehand and read in.
Depending on the number of output fields, calculation of interpolation
weights can require more CPU time than the time it takes to post the fields.
Obviously, operational Eta runs utilize pre-computed interpolation weights.
However, this is not necessary. The post retains the ability to compute
interpolation weights itself prior to posting fields. By stringing together
several control files the user may request that the same or different fields
be posted on different output grids. In turn, these different grids may
be in the same or different output files.
The simplest way to describe
the control file is by means of an example. Figure 8.2 shows a portion
of the operational Eta control file. A control file consists of three basic
components: the header, body, and end mark. In the header the user sets
the output grid type, the data set name, the data format, a new file flag,
output grid specifications, and two additional input/output flags. Following
the header, the user specifies which fields and levels to post. The post
processor has a fourth order smoother and a 25 point Bleck filter through
which data may be passed. The user controls these features by setting integer
switches in the body. The order in which the post processes requested output
fields is fixed by the code, but the order in which the user requests the
fields is irrelevant. The body of a control file only needs to list those
fields the user wants. To allow for this flexibility, every control file
must end with an end mark. The end mark line tells the post processor to
stop reading the control file and start posting requested fields.
The key to understanding the
header is remembering what the variable name at the start of each line
means. KGTYPE is a non-negative integer representing the type of output
grid. The convention here is to use Office Note 84 grid types with two
exceptions. The first exception is grid type 99999 which is the staggered
E grid, regardless of the horizontal resolution. The second exception is
grid type 00000. This grid type instructs the code to post the requested
field(s) on a filled E grid. In the upper portion of Fig. 7.2, grid type
94 is the 22km domain as defined in GRIB documentation (Office Note 388).
The string "START OF THIS OUTPUT GRID" is simply added for readability.
The post processor ignores everything in the header outside of the parentheses.
Each line of the header contains the data format the post expects to read.
Proper spacing is crucial.
Fig. 7.2. Portion of control
file from the operational Eta post.
DATSET is the root around
which the post creates output filenames. To this root the post appends
the format of the output file and the forecast hour xx as specified in
namelist FCSTDATA. Through the character string OUTYPE the user specifies
the data packing to be used when writing the output file. Two formats are
available: unpacked sequential binary and GRIB 1. Setting OUTYPE to NO
tells the post to write data using unformatted FORTRAIN writes. If DATSET
equals NOHEAD when OUTYPE equals NOPACK, no headers are written to the
binary output file. Otherwise, a grid header starts each file and each
output field is preceded by a record denoting the type and level of the
field. Setting OUTYPE to GRIBIT produces a GRIB 1 packed dataset.
When GRIB output is requested,
the two digit forecast time is appended to DATSET to form the the first
part of output filename. For example, if the environmental variable tmmark
in the running script for the Eta post processor (e.g. Fig. 7.3) is set
to tmyy, the first output file generated by the Eta post using the control
file in Fig. 7.2 is conventionally named EGDAWPxx.tmyy, where xx is the
forecast time and yy is equal 00 in the forecast and is negative in the
EDAS. For sequential binary output, .SbinFxx is appended to DATSET. Variable
NUFILE allows the user to specify whether fields requested in the body
are to be appended to a currently open output file or if a new output file
is to be opened. It is a simple YES/NO switch.
The indented variables in
the header deal with the output grid and pre-computed interpolation weights.
PROJ, NORTH, IMOUT, JMOUT, POLEI, POLEJ, ALATVT, ALONVT, and XMESHL are
the basic set of parameters by which standard NCEP software defines different
types of geographical grids. PROJ is a character*6 string denoting the
type of output grid projection. Three projections are currently supported:
POLA for polar stereographic, LOLA for latitude-longitude, and LMBC for
Lambert conformal conic. If the user wants grid relative winds on the native
model grid, PROJ must equal LOLA. NORTH is a logical flag for the northern
(. TRUE.) or southern (. FALSE.) hemisphere. (IMOUT, JMOUT) are the number
of west-east and south-north grid points (directions relative to the rotation
specified by ALONVT). Grid point (1,1) is in the southwest corner of the
grid; (IMOUT, JMOUT) in the northeast corner. POLEI and XMESHL define the
north-south and west-east grid increment on transformed grid respectively.
POLEJ and ALONVT are geodetic longitude and latitude of the center of the
E-grid. ALATVT is only required for Lambert conformal grids. It is the
latitude at which the projection is tangent to the surface of the earth.
The user may sidestep this
method to defining an output grid by setting READLL to YES. This tells
the post to read an input file containing the geodetic latitude (glat)
and longitude (glon) of output grid points. The post can read multiple
(glat,glon) files starting from unit number 30. The structure of the (glat,glon)
file expected by the post is ( ( (glat (i,j ),glon(i,j ) ), i=l, imout),
j=l, jmout) using FORMAT 5 (gl2.6, lx). This option of the post has not
been exhaustively tested since most users desire data on standard NCEP
grids.
Whenever the user is not posting
data on the model grid, it is recommended that interpolation weights be
pre-computed. The user tells the post to read an external weight file by
setting READCO to YES. If READCO equals NO the post processor will compute
all necessary interpolation weights prior to posting any fields. Source
code to pre-compute interpolation weights resides in ~wd22tb/etafcst/post/e2gd.
See the Read me files in this directory for details. The user must ensure
that the order in which interpolation weights are assigned in the template
is the order in which the grids are listed in the control file (see Section
1.5 for elaboration).
The bulk of the control file
is the body. This is where the user specifies which fields to post and
optionally the degree of smoothing or filtering to apply to the posted
fields. There are over 150 unique fields that may be posted from the Eta
model. This, of course, is subject to change in response to model development
and user needs. As mentioned above only those fields which are desired
need to be listed in the control file. Each field specification consists
of two lines. The first line, the identifier line, starts with a brief
description of the field. The post processor ignores this. Following this
are blocks Q= (xxx) and S= (xxx), which are now ignored by the code.
The SMTH block on the identifier
line controls the smoothing or filtering. In most applications the model
to output grid process involves two steps. First the staggered E grid is
filled to make a regular grid. This is then interpolated to the output
grid. Multiple pass smoothing or filtering of the data may be activated
at any of three places in this process. The first element of the SMTH block
activates a fourth order smoother that works on the staggered E grid. A
positive, nonzero integer tells the post to apply this smoother to the
field the indicated number of times. A more heavy handed multiple pass
smoother was found necessary to produce pleasing vorticity fields. Thus,
when smoothing a vorticity field, it is this smoother, not the fourth order
smoother, that is applied. Once data are on a regular grid a 25 point Bleck
filter may be applied in one of two possible places. The second integer
segment in the SMTH block controls the filtering of data on a filled E
grid. The last integer block of SMTH activates the Bleck filter on the
output grid. The Bleck filter is designed to remove scales smaller than
twice the grid separation. It has a fairly sharp response curve and will
largely preserve field maxima and minima even with several applications.
Following the identifier line
is the level line (L =) where the user requests data on particular levels.
There is room for output on as many as sixty levels. Some fields (e.g.,
total precipitation, shelter temperature, tropopause pressure) are single
level fields. For single level fields the integer 1 in the place immediately
following the left parenthesis activates output of the field. In general
the integer 1 activates output at a given level; 0 turns off output at
that level. However, there are exceptions which are noted below.
For isobaric fields (fields
for which S= 8) the pressure levels to which data may be posted are controlled
by namelist FCSTDATA read in at the start of an Eta model integration.
The order in which pressure levels are specified in FCSTDATA maps directly
to the left to right ordering of integers on the level line. For example,
using the FCSTDATA shown in Fig. 8.1, moving left to right across the level
line are pressure levels 50, 75, 100, 125, .... ,975, and 1000 mb. Fields
may be posted to different pressure levels by editing namelist FCSTDATA.
As a further example consider
the lines
(HEIGHT OF PRESS SFCS ) Q=(
1), S=( 8), SMTH=(00 02 02)
L=(11111 11111 11111 11111 11111
11111 11111 11110 00000 00000 00000 00000)
from Fig. 8.2. The field is
geopotential height on isobaric surfaces. The Q and S integers are set
for Office Note 84 packing. For each requested level two passes of the
Bleck filter will be applied to data on the filled E grid and the output
grid. Heights at all 39 isobaric levels as listed in Fig. 8.1 will be posted.
Two options are available for
data on constant eta layers. Setting the n-th integer on the level line
instructs the post to extract data on eta layer n. By "eta layer n" we
mean the n-th eta layer using the top down vertical indexing of the eta
model. At times it may be of interest to see what a selected field looks
like at the n-th atmospheric (i.e., above ground) eta layer. This is a
terrain following perspective. To activate this option, set the n-th integer
(left to right) on the level line to any integer between 2 and 9, inclusive.
For example, if a user wanted pressure data on the first, second, and fourth
atmospheric eta layers the settings could be
(PRESS ON ETA SFCS ) Q=( 8),
S=( 148), SMTH=(00 00 00)
L=(22020 00000 00000 00000 00000
00000 00000 00000 00000 00000 00000 00000)
In addition to eta layer and
isobaric level data, multiple levels may be requested for FD (Flight level)
fields and boundary layer fields. There are six FD levels. The ordering
on the level line is from the lowest (914 m MSL) to the highest (3658 m
MSL) FD level. Boundary layer fields are available from six 30 mb deep
layers. The ordering on the level line is from the lowest (nearest the
surface) to the highest constant mass layer. Two types of convective available
potential energy (CAPE) and convective inhibition (CIN) are available.
The first type (type one) starts the vertical integration from the lowest
above ground model layer. The second type (type two) searches the six 30mb
constant mass layers for the layer with the highest equivalent potential
temperature. The CAPE and CIN calculation then starts from this level using
this layer mean parcel. Type 1 CAPE and CIN are activated by setting the
leftmost integer on the level line to 1. The second leftmost integer controls
posting of type two CAPE and CIN. Both types may be requested. All other
fields are single level, meaning that the leftmost integer activates (1)
or deactivates (0) posting of that field.
The last section of a control
file is the end mark. This single line tells the post processor to stop
reading the control file and start posting requested fields. The key word
on the line is DONE. The post scans each line read from the control file
for this string. It is the only way to specify the end of a control file.
As shown in Fig. 8.2, individual
header-body-end control files may be chained together to output data in
numerous ways. The post reads the control files sequentially. If pre-computed
interpolation weights are to be read in, the user must ensure that their
assigned unit numbers correspond to the order in which the grids appear
in the combined control file. One last detail involves the end mark at
the end of the last control file. The post knows it has processed everything
when it reads an end of file mark (EOF) from the control file. This EOF
must immediately follow the last DONE statement. If not, the post will
unsuccessfully try to process what it thinks is the next set of control
cards.
7.5 The Template
The post processor was designed
to run as a stand-alone executable. Figure 8.3 shows a script that can
be used to run the Eta post processor on the IBM. The file itag is used
to specify the posting times for the Eta post processor. The file contains
three 2-digit numbers xx. The first two-digit number indicates the first
forecast time the user wishes to post, the second one is the interval between
the posting times, and the third one specifies how many forecast times
the user wishes to post. As shown in the template the post reads as input
(1) namelist FCSTDATA, (2) the constants nfile (nhb), (3) a restart file,
and (4) the control file.
Fig. 7.3. A script that
can be used to run the Eta post processor on the IBM.
7.6 Summary
We have described how to use
the Eta post processor in conjunction with the model. The post processor
was designed to run as a stand-alone executable. The user controls the
post by editing a control file. In this file the user specifies which fields
to post, smoothing options, data format, and output grids. When running
the product generator to output the grids on the non-native model grid
it is recommended to pre-compute interpolation weights.
While the post processor can
generate numerous output fields, it will never post every possible field.
Every user will eventually find need for some field not available from
the post. When the inevitable happens, several options exist.
First, any user can edit copies
of the model and post processor to generate the desired output fields.
The arrays needed to calculate the field must be added to the restart file
generated by the model. Subroutine CHKOUT writes the model restart file.
Post processor routine INITPOST which reads this file must be correspondingly
edited. The new field must also be added to the control file. Lastly, code
to generate the desired field must be added to the post processor. Where
this code is added is not particularly important. However, post processor
subroutine MISCLN has traditionally served this "catch-all" purpose. A
list of available posted fields can be found in the routine POSTDATA.f.
For those who do not wish
to tinker with the post processor code an alternative solution is to compute
the desired field(s) directly in the model. If this is deemed too expensive,
the model could simply write the information required to generated the
new field(s) to an output file. An external piece of code written by the
user would compute the new field(.s) from information in this output file.
If the user wanted to pack the new field(s) in GRIB 1, appropriately edited
versions post processor subroutines GRIBIT (and their supporting routines)
could be added to the user's post processor code.
Appendix 2: Product Generator
 ,
, ,
, .
. case of the eta coordinate. The reference pressure used in the Eta model
is
case of the eta coordinate. The reference pressure used in the Eta model
is  , where
, where 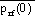 = 1013.25mb, To = 288K,
= 1013.25mb, To = 288K, 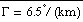 ,
, 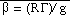 , g=9.8 m/s2, and R = 287.04J/K-kg. In the eta coordinate terrain assumes
a step-like appearance thereby minimizing problems associated with steeply
sloping coordinate surfaces. At the same time the coordinate preserves
the simplified lower boundary condition of a terrain following vertical
coordinate.
, g=9.8 m/s2, and R = 287.04J/K-kg. In the eta coordinate terrain assumes
a step-like appearance thereby minimizing problems associated with steeply
sloping coordinate surfaces. At the same time the coordinate preserves
the simplified lower boundary condition of a terrain following vertical
coordinate. ,
,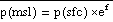 . The function
. The function 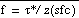 , where
, where 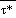 is the average of
is the average of  at the model surface and
mean sea level. The remaining question is how to determine these
at the model surface and
mean sea level. The remaining question is how to determine these 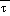 's.
's.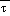 (sfc) and
(sfc) and 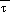 (msl) are first set using a 6.5
K/km lapse rate from the first sigma layer. A similar approach was not
successful in the Eta model due to the discontinuous nature of the step
topography. Virtual temperatures are averaged over eta layers in the first
60 mb above the model surface. The resulting layer mean virtual temperature
field is in turn horizontally smoothed before extrapolating surface and
sea level temperatures.
(msl) are first set using a 6.5
K/km lapse rate from the first sigma layer. A similar approach was not
successful in the Eta model due to the discontinuous nature of the step
topography. Virtual temperatures are averaged over eta layers in the first
60 mb above the model surface. The resulting layer mean virtual temperature
field is in turn horizontally smoothed before extrapolating surface and
sea level temperatures.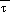 (sfc) and
(sfc) and 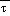 (msl) are subject to the Shuell
correction. Whether this correction is applied depends on the relation
of the extrapolated
(msl) are subject to the Shuell
correction. Whether this correction is applied depends on the relation
of the extrapolated 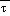 's to a critical value
's to a critical value 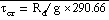 .
. (msl) exceeds
(msl) exceeds  cr, set
cr, set  (msl) to
(msl) to 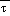 cr,
cr,
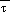 (sfc) and
(sfc) and 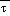 (msl) exceed
(msl) exceed 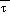 cr, set
cr, set 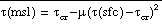 ,
,
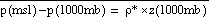 . This simple relationship itself can be used to obtain sea level pressure
given 1000 mb geopotential heights and an assumed mean density. In the
post, the mean density, ?*, is computed from
. This simple relationship itself can be used to obtain sea level pressure
given 1000 mb geopotential heights and an assumed mean density. In the
post, the mean density, ?*, is computed from 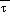 * and p* (the average in log pressure of p(sfc) and p(msl)).
* and p* (the average in log pressure of p(sfc) and p(msl)).
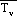 on each step inside the mountain (i.e., underground) are obtained by solving
a Laplace equation:
on each step inside the mountain (i.e., underground) are obtained by solving
a Laplace equation:
 .
. ,
,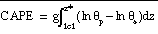

 , which shows the integrands to be related.
, which shows the integrands to be related.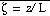 . The length
scale L is the Monin-Obukhov scale. A second important surface-layer parameter
is the flux Richardson number Rf. which quantifies the relative importance
of two production terms in the turbulent kinetic energy equation. Using
the Mellor-Yamada Level 2.0 model, Lobocki derived a fundamental equation
relating internal or surface-layer parameters
. The length
scale L is the Monin-Obukhov scale. A second important surface-layer parameter
is the flux Richardson number Rf. which quantifies the relative importance
of two production terms in the turbulent kinetic energy equation. Using
the Mellor-Yamada Level 2.0 model, Lobocki derived a fundamental equation
relating internal or surface-layer parameters  and Rf. with external or bulk characteristics of the surface-layer. Equations
consistent with this fundamental equation relating the wind speed, U, or
potential temperature,
and Rf. with external or bulk characteristics of the surface-layer. Equations
consistent with this fundamental equation relating the wind speed, U, or
potential temperature,  , between two levels,
z1 and z2, in the surface layer are
, between two levels,
z1 and z2, in the surface layer are .
.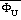 and
and 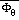 are integrated forms of similarity functions
for dimensionless differences of the quantity U or
are integrated forms of similarity functions
for dimensionless differences of the quantity U or  across the layer z1 to z2
across the layer z1 to z2 ,
, is a constant,
is a constant,  , and
, and 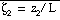 . The function
. The function 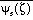 is given by equation (48)
in Lobocki's paper for S = U and (49) for S=
is given by equation (48)
in Lobocki's paper for S = U and (49) for S= .
.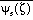 on the Monin-Obukhov height
on the Monin-Obukhov height  introduces a physically reasonable stability-based variability in computed
anemometer level winds and shelter temperatures. In the absence of strong
synoptic forcing both anemometer level winds and shelter temperatures exhibit
a typical diurnal cycle.
introduces a physically reasonable stability-based variability in computed
anemometer level winds and shelter temperatures. In the absence of strong
synoptic forcing both anemometer level winds and shelter temperatures exhibit
a typical diurnal cycle. .
.