Zoltan Toth, Olivier Talagrand, Guillem Candille and Yuejian Zhu

Draft (July 11, 2002)

7.1 Introduction

The previous chapters discussed verification procedures with respect to environmental predictions that are expressed in the form of a single value (out of a continuum) or a category. This chapter is devoted to the verification of probabilistic forecasts, typically issued for an interval or a category. Probabilistic forecasts differ from the previously discussed form of predictions in that, depending on the expected likelihood of forecast events, they assign a probability value between 0 and 1 to possible future states.

It is well known that all environmental forecasts are associated with uncertainty and that the amount of uncertainty can be situation dependent. Through the use of probabilities the level of uncertainty associated with a given forecast can be properly conveyed. Probabilistic forecasts can be generated through different methods. By considering a wide range of information, forecasters can subjectively prepare probabilistic forecasts. Alternatively, statistical techniques can be used either on their own, based on observational data (see, e. g., Mason and Mimmack, 2002; Chatfield, 2000), or in combination with a single dynamical model forecast and its past verification statistics (Atger, 2001). 

Probabilistic forecasts can also be based on a set of deterministic forecasts valid at the same time. Assuming the forecasts are independent realizations of the same underlying random process, the best estimate of the forecast probability of an event is equal to the fraction of the forecasts predicting the event among all forecasts considered. Ensemble forecasting, as this technique is called (see, e. g., Leith 1974; Ehrendorfer 1997), can thus produce probabilistic forecasts based on a set of deterministic forecasts, without necessarily relying on past verification statistics. In certain fields of environmental sciences, such as meteorology and hydrology, the ensemble forecasting technique is widely used. Therefore methods used to directly evaluate a set of ensemble forecasts, before they are interpreted in probabilistic terms, will also be discussed in this chapter. 

In the next section we will discuss the two main attributes of probabilistic forecasts, usually referred to as "reliability" and "resolution". Sections 7.3 and 7.4 will introduce a set of basic verification statistics that can be used to measure the performance of probabilistic forecasts for categorical and continuous variables with respect to these attributes. Section 7.5 is devoted to measures of ensemble performance, while section 7.6 discusses some limitations to probabilistic and ensemble verification. Some concluding remarks are found in section 7.7.

7.2. The Main Attributes of Probabilistic Forecasts: Reliability and Resolution.

How can one objectively evaluate the quality of probabilistic forecasts? Let us consider the following prediction: «There is a 40% probability that it will rain tomorrow». Assuming that the event 'rain' is defined unambiguously, it is clear that neither its occurrence nor its non-occurrence can be legitimately used to validate, or invalidate the prediction. Obviously, a probabilistic forecast cannot be validated on the basis of a single realization. This is in contrast with deterministic forecasts (?it will rain? or ?it will not rain?), which can be validated, or invalidated by one subsequent observation.

The only way to validate a forecast expressed in terms of probabilities is statistical. In the case above, one must wait until the 40 % probability forecast has been made a number of times, and then check the proportion of occurrences when rain was observed. If that proportion is equal or close to 40%, one can legitimately claim the forecast to be statistically correct. If, on the contrary, the proportion is significantly different from 40%, the forecast is statistically inconsistent.

One condition for the validity of probabilistic forecasts for the occurrence of an event is therefore statistical consistency between a priori predicted probabilities and a posteriori observed frequencies of the occurrence of the event under consideration. Consistency of this kind is required, for instance, for users who want to take a decision on the basis of an objective quantitative risk assessment (see chapter 8). Following Murphy (1973), this property of statistical consistency is called reliability. Reliability is the property that a probabilistic forecast is statistically valid.

Reliability, however, is not sufficient for a probabilistic forecast system to be useful. Consider the extreme situation where one would predict, as a form of probabilistic forecast for rain, the climatological frequency of occurrence of rain. That forecast system would be reliable in the sense that has just been defined, since the observed frequency of rain would be equal to the (unique) predicted probability of occurrence. But that system would not provide any forecast information beyond climatology. As a second condition, one requires that a forecast system reliably distinguish between cases with lower and higher than climatological probability values. After Murphy (1973), the ability of a forecast system to reliably vary forecast probability values is called resolution. Reliability and resolution together determine the usefulness of a probabilistic forecast system. There seems to be no desirable property of probabilistic forecast systems other that these two characteristics.

What has just been described for probabilistic prediction of occurrence of events easily extends to all forms of probabilistic prediction. Let us consider the quantity x (for instance, temperature at a given time and location), and a corresponding forecast probability density function p(x), represented by the full curve in Figure 7.1. For a particular case, the subsequent verifying observation value is shown by x_o (see Fig. 7.1). If, as in our example, x_o falls within the range of the forecast distribution, the observation does not validate or invalidate the forecast.The difficulty here is that, contrary to what happens with a single-value forecast (see chapter 5), it is not possible to define, in a trivial way, a 'distance' between the prediction (here the probability distribution p(x)) and the observation. Again, validation is possible only in a statistical sense. One must wait until the distribution p(x) is predicted a number of times, and then compare p(x) to the distribution p_o(x) of the corresponding verifying observations. If p_o(x) is identical with p(x) (or at least close to p(x) in some sense, as the distribution p₁(x) shown by the dash-dotted curve in Figure 7.1), then the prediction p(x) can legitimately be said to be statistically consistent, or correct. If, on the contrary, p_o(x) is distinctly different from p(x) (as the distribution p₂(x) shown by the dashed curve in the figure), then the prediction p(x) is statistically inconsistent.

This example calls for a more general definition of reliability. A system that predicts probability distributions is reliable if, for any forecast distribution p, the distribution of the corresponding verifying observations, taken when p was predicted, is identical to p. This definition can also be extended to multidimensional and any other type of probabilistic forecasts.

As noted earlier, reliability, albeit necessary, is not sufficient for the practical utility of a probabilistic forecast system. Systematic prediction of the climatological distribution of a meteorological variable is reliable yet it provides no added forecast value. Probabilistic forecasts should be able to reliably distinguish among sets of cases (through the use of a distinctly different forecast probability distribution, pⁱ, for each set) for which the distribution of corresponding observations (pⁱ_o) are distinctly different (and therefore also different from the climatological distribution). Such a system can ?resolve? the forecast problem in a probabilistic sense, and is called to have resolution. The more variations in probability values a forecast system can use in a reliable fashion, the more resolution it has. Maximum resolution is obtained if the forecast distributions are reliable and concentrated on one point, as Dirac functions. Note that a probabilistic forecast system generating perfectly reliable probabilistic forecasts at maximum resolution is actually a perfect categorical forecast system (see chapters 4 and 5). A probabilistic approach to forecasting is warranted when maximum resolution, due to the presence of uncertainties, is not attainable.

The two main attributes of probabilistic forecasts, reliability and resolution, are a function of both the forecasts and verifying observations. Sharpness is another characteristic of probabilistic forecast systems. Resolution was introduced above as reliable deviations of forecast probabilities from the climatological probabilities. Unlike resolution, sharpness is a function of the forecast (and not the observed) distributions only and it simply measures how different the forecast probability values are from climatological probabilities, irrespective whether those probabilities are consistent with the corresponding observations. It follows that one can easily make a probabilistic forecast sharper by bringing its shape closer to a Dirac function. Such an increase in the probability values for the mode of the distribution, however, generally will not enhance resolution. Resolution can be improved upon only through a clearer separation of situations where the event considered is more or less likely to occur as compared to the climatological expectation. 

Resolution thus cannot be improved via a simple change of probability values. Such improvements can be achieved only through the use of additional genuine knowledge about the behavior of the system that is being predicted, by changing the way groups of forecast cases are identified. This suggests that resolution, i. e., the ability to reliably identify cases with higher and lower than climatological expectancy, is in fact the intrinsic value of forecast systems. This becomes even clearer when the effect of statistical post-processing is considered on the other, complimentary attribute of probabilistic forecasts. Contrary to the case of resolution, reliability can be improved by simple statistical post-processing that modifies the forecast probability values. Let us assume, e. g., that the forecast distribution p(x) is associated with a distinctly different distribution of observations p₂(x) (dashed curve in Fig. 7.1). The next time the system predicts p(x), one can use p₂(x) as the calibrated forecast instead. This a posteriori calibration will make a forecast system, that was not so in the first place, reliable. For statistically stationary forecast and observed systems, perfect reliability can always be achieved, at least in principle, by such an a posteriori calibration. This, again, suggests that the intrinsic value of forecast systems lies not in their reliability (that can be made perfect through statistical adjustments) but in their resolution. 

In summary, a useful forecast system must be able to a priori separate situations into groups with as different outcomes as possible, represented by a distinct distribution of observations associated with each forecast group (resolution). If such a forecast system exists, the different forecast outcomes (groups of cases), even if originally designated differently, can be ?renamed? and marked by the observed distributions that are associated with them (reliability), based on a simple statistical verification and post-processing procedure. 

In the following section a number of scores that are used for the evaluation of binary, multi-categorical, and continuous variable probabilistic forecasts will be introduced. These scores will be systematically analyzed as to what they exactly measure in terms of reliability and resolution, and their significance will be illustrated using recent meteorological applications. In our analysis averages taken over all n available realizations of a probabilistic forecast system, or over a subset of cases satisfying a condition C will be denoted by E(.) and E_c(.) respectively.

7.3. Probabilistic Forecasts for Occurrence of Events.

In the following three subsections we will consider verification tools for the evaluation of probabilistic forecasts for the occurrence of a particular event E such as ?the temperature at a given location x at forecast lead time t will be less than 0 C?, or ?the total amount of precipitation over a given area and a given period of time will be more than 50 mm?. We denote by f(q) the observed frequency of occurrence of E in the circumstances when E is predicted to occur with probability q (0 # q# 1). The condition for reliability, as defined in the previous section, is that f(q) = q for all q.

7.3.1. The reliability curve.

As an example let us consider probabilistic forecasts based on the National Centers for Environmental Prediction (NCEP) Ensemble Forecast System (Toth and Kalnay, 1997) for the event of the 850-hPa temperature anomaly from the 1999 winter sample climatological mean value (T_c) being t = 4C or less. Diagnostics are accumulated over all grid-points located between longitudes 90W and 45E, and between latitudes 30N and 70N, and over 65 forecasts issued between 1 December 1998 and 28 February 1999, for a total of n=16,380 realizations. Forecast probability values are defined as i/m, where i (i = 0, ?, m) is the number of members that predicted the event out of an m=16 member ensemble. The forecast probabilities are thus discretized to m+1 = 17 predefined values. For deciding if the event occurred or not, the operational analysis of NCEP will be used as a proxy for truth (?verifying observation?).

The solid line in Fig. 7.2 shows a reliability curve, depicting variations of f(q) as a function of q, for the forecast system and event described above. Although rather close to the diagonal f(q) = q, the reliability curve shows some deviations from it. In particular, the slope of the reliability curve in Fig. 7.2 is below that of the diagonal. Note that deviations from the diagonal are not necessarily indicative of poor reliability. When statistics, like in our example, are based on a finite sample the reliability curve for even a perfectly reliable forecast system would exhibit fluctuations around the diagonal. The effect of sampling variability can be quantified by verifying the same ensemble again except this second time against one of its randomly chosen members. In this setup, by definition, the forecast system is perfectly reliable and any deviations from the diagonal are due to sampling fluctuations caused by the finite volume of data. When compared to the diagonal, the difference between the perfect (dash-dotted line in Fig. 7.2) and operational ensemble curve (solid line) reflect the actual lack of reliability in the forecast system, irrespective of the size of the verification sample.

The bar graph in the lower right corner of Figure 7.2 is known as a sharpness graph, and shows the frequency p(q) with which each probability q is predicted. The 0 and 1 probability values are used in 90% of the realizations of the process. This means that, at the 2-day range considered here, the dispersion of the predicted ensembles is relatively small so that in most cases all forecast temperature values in the ensemble fall on the same side of the threshold T_c + t that is used to define the event. In a quantitative evaluation of the performance of the forecast, the two extreme points p =0 and p =1 must therefore be given proportionately more weight.

7.3.2. The Brier Score.

Brier (1950) proposed the following measure for the quantitative evaluation of probabilistic forecasts for the occurrence of a binary event:(7.1)

where n is the number of realizations of the forecast process over which the validation is performed. For each realization j, q_j is the forecast probability of the occurrence of the event, and o_j is a binary observation variable that is equal to 1 or 0 depending on whether the event occurred or not.

The Brier score for a deterministic system that can perfectly forecast the occurrence or non-occurrence of events with q=1 or 0 respectively assumes a minimum value of 0. On the contrary, the Brier score for a systematically erroneous deterministic system that predicts probability 0 when the event does, and 1 when it does not occur would assume a maximum value of 1. 

For comparing the Brier score to that of a competing reference forecast system (B_ref) it is convenient to define the Brier Skill Score (BSS): 

BSS=1-B/B_ref                                        (7.2)

Contrary to the Brier score (7.1), the Brier Skill Score is positively oriented (i.e., higher values indicate better forecast performance). BSS is equal to 1 for a perfect deterministic system, and 0 (negative) for a system that performs like (poorer than) the reference system. Most often climatology is used as a reference system. For a climatological forecast system, i.e. a system that always predicts the climatological frequency of occurrence p_c of an event, o assumes the value 1 with frequency p_c, and the value 0 with frequency 1- p_c. The Brier score is then:B_c= p_c(1- p_c). Such a system, as discussed before, has perfect reliability, but no resolution. In the rest of this chapter, the Brier Skill Score will be defined with the climatological forecast system as a reference (BSS_c=1-B/B_c).

For facilitating the forthcoming discussion, continuous variables are introduced as:

(7.3)

where p(q) is the frequency with which q is predicted. In realistic forecast situations the number of distinct forecast probability values is finite and the integral in (7.3) reduces to a finite sum. Since when q is predicted the event occurs with frequency f(q), the climatological frequency of occurrence of the event is

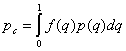(7.4)

More generally, integration with respect to p(q) is identical with averaging over all realizations of the forecast process for any quantity u:

(7.5)

The statistical performance of a system for probabilistic prediction of occurrence of an event is entirely determined by the corresponding functions p(q) and f(q). Different prediction systems will correspond with different functions of p(q) and f(q), while the climatological frequency of occurrence p_c, that is independent of the prediction system, will in all cases be given by Eq. (7.4).

From now on, we will systematically express scores as explicit functions of p(q) and f(q). On partitioning the average in Eq. (7.1) according to the forecast probability q, the Brier score B reads

(7.6)

For given q, o assumes a value of 1 with frequency f(q), and 0 with frequency 1- f(q). Therefore

E[(q-o)²½q] = (q-1)² f(q) + q² [1-f(q)]

=[q-f(q)]² + f(q) [1-f(q)](7.7)

from which we obtain, upon integration with respect to p(q) dq, and by using Eq. (7.4)

(7.8)

The Brier score is thus decomposed into three terms, each with its own significance (Murphy 1973). The first term on the right hand side of Eq. (7.8), that is a weighted measure of the departure of the reliability curve from the diagonal (see Fig. 7.2), is a measure of reliability. We recall that for an ideal forecast system where events are observed with the same frequency as they are forecast (f(q)= q) this term is zero. The second term (with a negative sign) is a measure of how different the observed frequencies corresponding to the different forecast probability values are from the climatological frequency of the event. The larger these differences are, the better the forecast system can a priori identify situations that lead to the occurrence or non-occurrence of the event in question in the future. This term is a measure of resolution as defined in section 7.2. It is independent of the actual forecast probability values (and thus also independent of reliability), and is only a function of how the different forecast events are classified (or ?resolved?) by a forecast system. The third term on the right hand side of Eq. 7.8 is independent of the prediction system and is a function of the climatological uncertainty only. The difficulty (or lack of it) of predicting events with close to 0.5 (0 or 1) climatological probability is recognized by a large (small) uncertainty term in Eq. 7.8.

The scores(7.9a)

and

(7.9b)

will be used to measure reliability and resolution respectively. Both scores are negatively oriented, and are equal to 0 for a perfect deterministic system. Like the Brier Skill Score BSS (Eq. 7.2), they are comparable for events with different climatological frequencies of occurrence. They are related to the Brier Skill Score (defined using the climatological forecast system as a reference, BSS_c) by the equality

BSS_c = 1 - (B_Rel + B_Res)(7.10)

The Brier score B for the operational NCEP system represented by the solid curve in Figure 7.2 is equal to 0.066. The climatological frequency of occurrence p_c for the event under consideration is equal to 0.714, which gives a value of 0.677 for the Brier Skill Score BSS_c. This corresponds to B_Rel = 0.027 and B_Res = 0.296. These values are rather typical of the values produced by present short- and medium- range Ensemble Prediction Systems. The fact that the reliability term is significantly smaller (typically one order of magnitude less) than the resolution term is generally observed. This fact, however, has no particular meaning since, as pointed out earlier, reliability and resolution are two different and independent aspects of forecast quality.

Figure 7.3 shows the Brier Skill Score defined using the climatological forecast system BSS_c (full curve) and its two components B_Rel (short-dashed curve) and B_Res (dashed curve), as a function of forecast lead time, for the European Centre for Medium-range Weather Forecasts (ECMWF) Ensemble Prediction System (Molteni et al. 1996). The event considered here is that the deviation of the 850-hPa temperature from its 1999 winter mean (sample climatology T_c) is less than t = 2C. Scores were computed over the same geographical area and time period as those used to construct Figure 7.2. Since no data were missing, the total number of cases considered is now n = 22,680. Forecast probabilities are defined, as in the case of Figure 7.2, as i/m (i = 0, ?, m=50), and the verifying 'observation' is the ECMWF operational analysis.

The score BSS_cnumerically decreases (meaning the quality of the system degrades) with increasing forecast range. The decrease is entirely due to the resolution componentB_Res, whereas the reliability component B_Rel (which, as before, is significantly smaller than B_Res) shows no significant variation. The degradation of resolution corresponds to the fact that, as the lead-time increases, the forecast ensemble has a broader dispersion, and becomes more similar to the climatological distribution. All these features are typical of current Ensemble Prediction Systems.

Finally we note again that if both the forecast and observed systems are stationary in time and there is a sufficiently long record of their behavior it is possible to make an imperfect forecast system completely reliable (see also section 7.2). If the frequency of occurrence of an event (f(q)) is different from the forecast probability, the latter can be calibrated by a posteriori changing it to f(q). This, if done on all values of q, amounts to moving all points of the reliability curve horizontally to the diagonal (Figure 7.2). As a result of this calibration, the first term on the right hand side of Eq. (7.8) becomes 0, while the second term, that measures the variations of the observed frequencies f(q) around the climatological frequency as the forecast probability q changes, is not modified. The observed frequencies f(q) are thus the probabilities that can be effectively used by a forecast system, following an a posteriori calibration. As mentioned earlier, resolution cannot be improved through such a simple statistical correction of the forecast probability values. This confirms that it is the resolution part of the Brier score that measures a forecast system?s genuine ability to distinguish among situations that lead to the future occurrence or non-occurrence of an event.

7.3.3. Relative Operating Characteristics

Another commonly used score for evaluating probabilistic forecasts of occurrence of binary events is called the Relative Operating Characteristics (or Receiver Operating Characteristics, Bamber, 1975), usually abbreviated as ROC.

A Relative Operating Characteristics graph is based on a set of contingency tables used to evaluate deterministic forecasts for the occurrence of a binary event. A contingency table is built by separating the realizations of the system into four classes depending on whether the event under consideration is predicted to occur or not, and on whether it actually occurs or not (see also Chapter 3):

Observed
 

	Yes	No
Yes	A	B
No	C	D

Forecast

where A, B, C, and D are the number of realizations in each of the four classes. In particular, the ratio

(7.11a)

is the proportion of 'hits', i. e., of correctly predicted occurrences of the event. The ratio

(7.11b)

is the proportion of 'false alarms', i. e., of situations in which the event is incorrectly predicted to occur.

The Relative Operating Characteristics curve for a probabilistic prediction system for the occurrence of an event is then defined as follows. For each threshold value s, 0 # s# 1, the probabilistic prediction is transformed into a deterministic prediction by issuing a ?yes? forecast for the event if p is greater than s, and a ?no? forecast otherwise. An m-member ensemble, for example, can be fully described by the use of m thresholds (corresponding to the distinct forecast events of at least 1, 2, 3, ..., or m members predicting an event). The hit and false alarm rates (Eq. 7.11) for the different values of s define the ROC curve. 

When the event is always predicted (s = 0, or strictly speaking, s < 0, C = D = 0) then H = F = 1. At the other extreme, when the event is never predicted (s = 1, A = B = 0) H = F = 0. For any forecast system both H(s) and F(s) decrease from 1 to 0 when s increases from 0 to 1. The ROC curve for a climatological system that always predicts the climatological frequency of occurrence p_c is defined by the two points H(s) = F(s) = 1 for s < p_c, and H(s) = F(s) = 0 for s$ p_c. In case of a deterministic forecast system (m=1) there is only one decision criterion and the ROC curve is defined by the corresponding point, along with the points at the end of the diagonal (H = F = 1, H = F = 0). For a perfect deterministic system (B = C = 0) H(s) = 1 and F(s) = 0. A probabilistic forecast system with good reliability and high resolution is similar to a perfect deterministic forecast in that it will use probabilities that are all close to either 0 or 1. For such a system all (F(s), H(s)) points will therefore be close to the optimal (0,1) point for a large range of values of s. It follows that in general the proximity of the ROC curve to the point (0, 1) is an indicator of the value of a forecast system. Therefore the area below the curve in the (F, H)-plane is an overall quantitative measure of forecast value. 

A more detailed analysis of the significance of ROC results can be given by first realizing that the relative frequency of hits in Table 7.1 (A) for a given probability threshold scan be written, using earlier introduced notation, as: 

Note also that the sum A + C is equal to the climatological frequency of occurrence p_c. Therefore the hit rate can be written as:

(7.12a)

A similar argument shows that the false alarm rate can be written as 

(7.12b)

The integral in (7.12a) is the average of f(q) for those circumstances when q > s. If f(q) is a strictly increasing function of q, that last inequality is equivalent to f(q) > f(s), and the comparison with the threshold can be done on the a posteriori calibrated probabilities f as well as on the directly predicted probabilities q. The same argument applies to the integral in (7.12b), which means that the ROC curve is invariant to the a posteriori calibration through which the points in the reliability curve are moved horizontally to the diagonal. Thus, if the calibrated forecast probability values f(q) are strictly increasing with the original forecast probabilities q, the ROC curve, just like the resolution component of the Brier score, depends only on the a posteriori calibrated probabilities f (and their frequency distribution). The ROC curve is therefore an indicator of the resolution of the prediction system and is independent of reliability. The resolution component of the Brier score and the ROC curve therefore provide very similar qualitative information. 

As an example, ROC curves are displayed in Fig. 7.4 for the same event and forecast system as that studied in Fig. 7.3. Note that, as expected, the ROC-area defined by the curves monotonically decreases as a function of increasing forecast lead time (with values of 0.977, 0.952, 0.915 and 0.874 for 2, 4, 6 and 8 days lead time respectively), just as the Brier score does in Fig. 7.3. While there is a qualitative agreement in that both theROC and Brier scores indicate a loss of predictability with increasing lead time, the corresponding values for the two scores are quantitatively different. Moreover, there is no one-to-one relationship between the two measures. It is not clear at present which measure of resolution, if either, is preferable for any particular application. We note that the potential economic value associated with the use of a forecast system is measured through the same contingency table (Table 7.1) as that used to define ROC (see chapter 8).

7.3.4. Information content

It has been argued that probabilistic forecasts made by and for stationary processes can, at least theoretically, be made fully reliable through post-processing. It was also pointed out that the real value of forecasts lies in their resolution. In this subsection, following Toth et al. (1998) we introduce information content (I) as another statistic to measure the resolution of reliable probabilistic forecasts. As an example, let us consider a set of 10 climatologically equally likely intervals as predictands. In this case it is convenient to define information content (I) in the forecast based on log₁₀ in the following way:

(7.13)

where p_iis the forecast probability of the i'th category. We require that and 0# p_i#1 for all p_i. If the forecasts are perfectly reliable, I can be considered as another measure of resolution. Under these conditions I varies between 0 (for a climatological forecast distribution) and 1 (for a deterministic forecast distribution). I can be arithmetically averaged over a set of forecast cases. Fig. 7.5 shows the information content of a 10-member 0000 UTC subset of the NCEP ensemble for 500 hPa height values as a function of lead-time. For further examples on how the concepts of information theory can be used in probabilistic forecast verification, the readers are referred to Stevenson and Doblas-Reyes (2000), and Roulston and Smith (2002).

7.3.5 Multiple-outcome events

The Brier score (7.1) was defined above for the evaluation of probabilistic forecasts for the occurrence or non-occurrence of a single binary event. While in many studies the Brier score is used as in Eq. 7.1, in his original paper Brier (1950) gave a more general definition, considering multiple-outcome events. Let us consider an event with K complete, mutually exclusive (and not necessarily ordered) outcomes E_k (k = 1, ?, K), of which one, and only one, is always necessarily observed (e. g., 4 categories such as no precipitation, liquid, frozen, or mixed precipitation). A probabilistic prediction for this set of events then consists of a sequence of probabilities q = (q_k), k = 1, ?, K, with S_k q_k = 1. The score defined by Brier is

B_K = (1/K) E[ S_k=1,K (q_k-o_k)² ] = (1/K) E[½½q - o ½½² ](7.14)

where o_k = 1 or 0 depending on whether the observed outcome is E_k or not. On the right hand side of Eq. 7.14 ½½.½½ denotes the Euclidean norm, ando is the sequence (o_k). B_K is the arithmetic average of the Brier scores (7.1) defined for the various outcomes E_k, each considered as binary events. A skill score, similar to (7.2) can be defined as

BSS_K = 1 - B_K / B_refK

The reference Brier score (B_refK), for example, can be computed for the climate forecast system that systematically predicts p_ck for each k: B_cK = (1/K) S_k p_ck(1- p_ck), where p_ck is the climatological frequency of the occurrence E_k. Examples for the use of the multi-event Brier score can be found in Zhu et al. (1996) and Toth et al. (1998).

A reliability-resolution decomposition of the score B_K can be defined by averaging the decompositions of the elementary scores for the occurrences E_k. For multi-event forecasts, a more discriminatory decomposition, built on the entire sequence q of predicted probabilities, seems preferable. Denoting dp(q) the frequency with which the sequence q is predicted by the system, and defining the sequence f(q) = [f_k(q)] of the conditional frequencies of occurrence of the E_k's given that q has been predicted, a generalization of the derivation leading to Eq. (7.8) shows that

(7.15)

where p_c is the sequence (p_ck). Similarly to Eq. (7.8),Eq. (7.15) provides a decomposition of B_K into reliability, resolution, and uncertainty terms.

7.4. Probabilistic Forecasts for a Numerical Variable.

While the previous section presented basic verification tools for evaluating single or multiple category binary events, here we discuss how probabilistic forecasts for a numerical variable x, such as temperature given at a point at a particular time, can be evaluated. Such a probabilistic forecast consists of a full probability distribution, instead of one, or a finite number of probability values. In any practical application, the probability distribution will of course be still defined by a finite number of numerical values. Note that the discretization here is needed only for carrying out the numerical calculations, and is not imposed as a constraint arising due to the format of the forecasts.

7.4.1 The Discrete Ranked Probability Score

Let us define J thresholds x_j (j =1, ?, J), x₁ < x₂ < ?< x_J, for the variable x, and the associated J events H_j = (x ? x_j), (j = , ?, J). A probability distribution for x defines a sequence of probabilities p₁ ? p₂ ? ?? p_J for those events. The quantity o_j is defined for each j as being equal to 1 or 0 depending on whether the event H_j is observed to occur or not. The discrete Ranked Probability Score (RPS) is then defined as

(7.16)

where B(x_j) is the Brier score (7.1) relative to the event H_j.

The Ranked Probability Score is similar to the multi-event Brier score (7.13), but, as its name implies, it takes into account the ordered nature of the variable x. Here the events H_j are not mutually exclusive, and H_j implies H_j' if j < j'. Consequently, if x is predicted to fall in an interval [x_j, x_j+1] with probability 1, and is observed to fall into another interval [x_j', x_j'+1], the RPS increases with the increasing absolute difference ½j-j'½.

7.4.2 The Continuous Ranked Probability Score

An extension of the RPS can be definedby considering an integral of the Brier scores over all thresholds x, instead of an average of Brier scores over a finite number of thresholds as in (7.16). We denote by F(x) the forecast probability distribution function, and x_Othe verifying observation. By choosing a measure m(x) for performing the integral, the Continuous Ranked Probability Score (CRPS) reads as: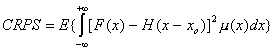(7.17)

where H is the Heaviside function (H(x) = 0 if x < 0, H(x) =1 if xC0).

Boththediscrete and continuous Ranked Probability Scores, just like the multi-event Brier score (7.14), can be expressed as skill scores (see Eq. 7.2), and are amenable to a reliability-resolution decompositions. For additional related information the reader is referred to Hersbach (2000). Further details on some of the other scores discussed in sections 7.3 and 7.4 can also be found in Stanski et al. (1989).

7.5 Ensemble statistics

An ensemble, in general, is a collection of forecasts that sample the uncertainty in the initial and forecast state of the system. At initial time, the ensemble is centered at the best estimate of the state of the system (that can be obtained either directly or by averaging an ensemble of analysis fields, and will be called the control analysis). As discussed earlier, ensemble forecasts are used widely for the generation of probabilistic forecasts. The previous section was devoted to the verification of probabilistic forecasts in general. Before ensemble forecasts are converted into probabilistic information, however, it is desirable to evaluate their basic characteristics. 

In section 7.3 it was pointed out that the inherent value of forecast systems lies in their ability to distinguish between cases when an event has a higher or lower than climatological probability to occur in the future (resolution), based on the initial conditions. As Figs. 7.3 and 7.4 demonstrate, in chaotic systems resolution is limited in time. This is because in such systems naturally occurring instabilities amplify initial and model related uncertainties. Even though skill is reduced and eventually lost, forecasts can remain (or can be calibrated to remain) statistically consistent with observations (reliability).

An ensemble forecast system that is statistically consistent with observations is often called a perfect ensemble in a sense of perfect reliability. An important property of a perfectly reliable ensemble is that the verifying analysis (or observations) should be statistically indistinguishable from the forecast members. Most of the verification tools specifically developed and applied on ensemble forecasts are designed to evaluate the statistical consistency of such forecasts. These additional measures of reliability, as we will see below, can reveal considerably more detail as to the nature and causes of statistically inconsistent behavior of ensemble-based probabilistic forecasts than the reliability diagram (section 7.3.1) or the one-dimensional metric of the reliability component of the Brier score (section 7.3.2) discussed above. By revealing the weak points of ensemble forecast systems, the ensemble-based measures provide important information to the developers of such systems that eventually can lead to improved probabilistic forecasts as well.

7.5.1Ensemble mean error and spread

If the verifying analysis is statistically indistinguishable from the ensemble members then its distance from the mean of the ensemble members (ensemble mean error) must be statistically equal to the distance of the individual members from their mean (ensemble standard deviation or spread, see, e. g., Buizza 1997). Fig. 7.6 contrasts the root mean square error (see chapter 5) and spread of the NCEP ensemble mean forecast as a function of lead time. Initially, the ensemble spread is larger than the ensemble mean error, indicating a larger than desired initial spread. The growth of ensemble spread, however, is below that of the error, which leads to insufficient spread at later lead times. This is a behavior typical of current ensemble forecast systems that do not properly account for model related uncertainties.

For reliable forecast systems the ensemble mean error (that is equal to the spread in the ensemble) can also be considered as a measure of resolution (and therefore forecast skill in general). For example, an ensemble with a lower average ensemble spread can more efficiently separate likely and unlikely events from each other (and also has more forecast information content). The ensemble mean forecast can also be compared to a single forecast started from the same control analysis around which the initial ensemble is centered (control forecast). Once nonlinearities become pronounced the mean of an ensemble that properly describes the case dependent forecast uncertainty should provide a better estimate of the future state of the system than the control forecast (see Toth and Kalnay 1997) that generally can fall anywhere within the cloud of the ensemble. In a properly formed system ensemble mean error, thus, should be equal to or less than the corresponding control forecast error, as seen in Fig. 7.6. 

7.5.2 Equal likelihood histogram

Ensemble forecast systems are designed to generate a finite set (m) of forecast scenarios. Some ensemble forecast systems (e. g., those produced by ECMWF and NCEP) use the same technique for generating each member of the ensemble (i. e., same numerical prediction model, and same initial perturbation generation technique). In other cases each ensemble member is generated by a different model version (like in the ensemble at the Canadian Meteorological Centre, see Houtekamer et al. 1996). In such cases individual ensemble members may not perform equally well. Similarly, if the control forecast is included in an otherwise symmetrically formed ensemble, the issue of equal likelihood arises. 

Whether all ensemble members are equally likely or not is neither a desirable nor an undesirable property of an ensemble in itself. When ensemble forecasts are used to define forecast probabilities, however, one must know if all ensemble members can be treated in a symmetric fashion. Whether all ensemble members are equal can be tested by generating a histogram showing the number of cases (accumulated over space and time) when each member is closest to the verifying diagnostic (analyzed or observed state, see Zhu et al. 1996). Information from such a histogram can be useful as to how the various ensemble members must be used in defining forecast probability values. A flat (uneven) histogram, for example, indicates that all ensemble members are (not) equally likely and can (cannot) be considered as independent realizations of the same random process, indicating that the simple procedure used in section 7.3.1 for converting ensemble forecasts into probabilistic information is (not) applicable.

Fig. 7.7 contrasts the frequency of NCEP ensemble forecasts being best (i. e., closest to the verification, averaged for 10 perturbed ensemble members) with that of an equal and a higher resolution unperturbed control forecast as a function of lead-time. Note first in Fig. 7.7 that the high resolution control forecast, due to its ability to better represent nature, has an advantage against the lower resolution members of the ensemble. This advantage, however, is rather limited. As for the low resolution control forecast, at short lead times, when the spread of the ensemble around the control forecast is too large (see Fig. 7.6), it is somewhat more likely to be closest to the verifying analysis. At longer lead times, when the spread of the NCEP ensemble becomes deficient due to the lack of representation of model related uncertainty, the control forecast becomes less likely to verify best. When spread is too low, the ensemble members are clustered too densely and the verifying analysis often lies outside of the cloud of the ensemble. In this situation, since the control forecast is more likely to be near the center of the ensemble cloud than the perturbed members, a randomly chosen perturbed forecast has a higher chance of being closest to the verifying observation than the control. The flat equal likelihood histogram at intermediate lead times (indicated by the 48-hour perturbed and equal resolution control forecasts having the same likelihood in Fig. 7.7) thus is also an indicator of proper ensemble spread (cf. Fig. 7.6), and hence close to perfect reliability.

7.5.3 Analysis rank histogram

If all ensemble members are equally likely and statistically indistinguishable from nature (i. e., the ensemble members and the verifying observation are mutually independent realizations of the same probability distribution), then each of the m+1 intervals defined by an ordered series of m ensemble members, including the two open ended intervals, is equally likely to contain the verifying value. Anderson (1996) and Talagrand et al. (1998) suggested constructing a histogram by accumulating the number of cases over space and time when the verifying analysis falls in any of the m+1 intervals. Such a graph is often referred to as the "analysis rank histogram".

Reliable or statistically consistent ensemble forecasts lead to an analysis rank histogram that is close to flat, indicating that each interval between the ordered series of ensemble forecast values is equally likely (see 3-day panel in Fig. 7.8). An asymmetrical distribution is usually an indication of a bias in the first moment of the forecasts (see 15-day lead time panel in Fig. 7.8) while a U (5-day panel in Fig. 7.8) or inverted U-shape (1-day panel in Fig. 7.8) distribution may be an indication of a positive or negative bias in the second moment (variance) of the ensemble respectively. Current operational NWP ensemble forecast systems in the medium lead-time range exhibit U-shaped analysis rank histograms, which is an indication that more often than expected by chance due to the finite ensemble size, the cloud of the ensemble misses to encompass the verifying analysis. 

7.5.4 Multivariate statistics

All ensemble verification measures discussed so far are based on the accumulation of statistics computed over single grid-points. An ensemble system that is found statistically consistent in this manner, however, will not necessarily produce forecast patterns that are consistent with those observed (or analyzed). Recently, various multivariate statistics have been proposed to evaluate the statistical consistency of ensemble forecasts with analyzed fields in a multivariate manner.

One approach involves the computation of various statistics (like average distance of each member from the other members) for a selected multivariate variable (e. g., 500 hPa geopotential height defined over grid-points covering a pre-selected area), separately for cases when the verifying analysis is included in, or excluded from the ensemble. A follow-up statistical comparison of the two, inclusive and exclusive sets of statistics accumulated over a spatio-temporal domain can reveal whether at a certain statistical significance level the analysis can be considered part of the ensemble in a multivariate sense (in case the two distributions are indistinguishable) or not. Smith (2000) suggested the use of the nearest neighbor algorithm for testing the statistical consistency of ensembles with respect to multivariate variables in this fashion.

Another approach is based on a comparison of forecast error patterns (e. g., control forecast minus verifying analysis) and corresponding ensemble perturbation patterns (control forecast minus perturbed forecasts). In a perfectly reliable ensemble, the two sets of patterns are statistically indistinguishable. The two sets of patterns can be compared either in a climatological fashion, based, for example, on an empirical orthogonal function analysis of the two sets of patterns over a large data set (for an example, see Molteni and Buizza 1999), or on a case by case basis (see Wei and Toth 2002). 

7.5.5 Time consistency histogram

The concept of rank histograms can be used not only to test the reliability of ensemble forecasts but also to evaluate the time consistency between ensembles issued on consecutive days. Given a certain level of skill as measured by the probabilistic scores discussed in section 7.3, an ensemble system that exhibits less change from one issuing time to the next may be of more value to some users. When constructing an analysis rank histogram, in place of the verifying analysis one can use ensemble forecasts generated at the next initial time. The "time consistency" histogram will assess whether the more recent ensemble is a randomly chosen subset of the earlier ensemble set. 

Ideally, one would like to see that with more information, newly issued ensembles narrow the range of the possible, earlier indicated solutions, without shifting the new ensemble into a range that has not been included in the earlier forecast distribution. Such "jumps" in consecutive probabilistic forecasts would result in a U-shaped time consistency histogram, indicating sub-optimal forecast performance. While control forecasts, representing a single scenario within a large range of possible solutions, can exhibit dramatic jumps from one initial time to the next, ensembles typically show much less variations.

7.6Limitations

The verification of probabilistic and ensemble systems, as that of any other kind of forecasts, has its limitations. First, as pointed out earlier, probabilistic forecasts can be evaluated only in a statistical sense. The larger the sample size, the more stable and trustworthy the verification results become. Given a certain sample size, one often needs to, or has the option to subdivide the sample in search for more detailed information. For example, when evaluating the reliability of continuous-type probability forecasts one has to decide when two forecast distributions are considered being the same. Grouping more diverse forecast cases into the same category will increase sample size but can potentially reduce useful forecast verification information. 

Another example concerns spatial aggregation of statistics. When the analysis rank or other statistics is computed over large spatial or temporal domains a flat histogram is a necessary but not sufficient condition for reliability. Large and opposite local biases in the first and/or second moments of the distribution may get canceled out when the local statistics are integrated over larger domains (see, e. g., Atger 2002). In a careful analysis, the conflicting demands for having a large sample to stabilize statistics, and working with more specific samples (collected for more narrowly defined cases, or over smaller areas) for gaining more insight into the true behavior of a forecast system, need to be balanced.

So far it has been implicitly assumed that observations are perfect. To some degree this assumption is always violated. When the observational error is comparable to the forecast errors observational uncertainty needs to be explicitly dealt with in forecast evaluation statistics. A possible solution is to introduce the same noise on the ensemble forecast values as the observations have (Anderson 1996).

In case of verifying ensemble-based forecasts, one should also consider the effect of ensemble size. Clearly, a forecast based on a smaller ensemble will provide a noisier and hence poorer representation of the underlying processes, given the forecast system studied. Therefore special care should be exercised when comparing ensembles of different sizes.

The limitations described above must be taken into account not only in probabilistic and ensemble verification studies, but also in forecast calibration where probabilistic and/or ensemble forecasts are statistically post-processed based on forecast verification statistics.

7.7 Concluding remarks

In this chapter we have reviewed various methods for the evaluation of probabilistic and ensemble forecasts. Reliability and resolution were identified as the two main attributes of probabilistic forecasts. Reliability is a measure of statistical consistency between probabilistic forecasts and the corresponding distribution of observations over the long run, while resolution measures how different the probability values in perfectly reliable forecasts are from the background (climatologically derived) probability values. The ideal forecast system uses only 0 and 1 probability values and has a perfect reliability. Note that this is a perfect dichotomous (non-probabilistic) forecast system, i. e., a deterministic forecast is a special case of probabilistic forecasts, one without uncertainty. 

In the course of verifying probabilistic forecasts, their two main attributes: reliability and resolution are assessed. Such a verification procedure, just as that of any other type of forecasts, has its limitations. Most importantly we recall that probabilistic forecasts can only be evaluated on a statistical (and not individual) basis, preferably over a large sample. When a stratification of all cases is warranted, a compromise has to be found between the desire to learn more details about a forecast system and the need for maintaining large enough sub-samples to ensure the stability of verification statistics. Additional limiting factors include the presence of observational error, and to a lesser extent, the use of ensembles of limited size. The issue of comparative verification, where two forecast systems are inter-compared, was also raised and the need for the use of benchmark systems, against which a more sophisticated system can be compared, was stressed.

It was also pointed out that for temporally stationary forecast and observed systems the reliability of forecasts can be made, at least theoretically, perfect through a calibration procedure based on past verification statistics. In contrast, resolution cannot be improved in such a simple manner. Thus measuring the resolution of calibrated forecasts can provide sufficient statistics for the evaluation of probabilistic forecasts.

The relationship among the different verification scores like the Ranked Probability Skill Score, the Relative Operating Characteristics, and the information content that for perfectly calibrated probabilistic forecasts measures the same attribute, resolution, is not clearly understood. Which scores are best suited for certain applications is not clear either. It is important to mention in this respect that the value of environmental forecasts can also be assessed in the context of their use by society. The economic value of forecasts has such significance that an entire chapter (Chapter 8) is devoted to this subject. We close the present chapter by pointing out that some of the verification scores discussed above have a clear link with the economic value of forecasts. For example, the resolution component of the Brier skill score, and the ROC-area, two measures of the resolution of forecast systems, are equivalent to the economic value of forecasts under certain assumptions(Murphy 1966; Richardson 2000).

6. REFERENCES

Anderson, J. L., 1996: A method for producing and evaluating probabilistic forecasts from ensemble model integrations, J. Climate, 9, 1518-1530.

Atger, F., 2001: Verification of intense precipitation forecasts from single models and ensemble prediction systems. Nonlinear Processes in Geophysics, 8,401 - 417. 

Atger, F., 2002: Spatial and interannual variability of the reliability of ensemble based probabilistic forecasts: Consequences for calibration. Mon. Wea. Rev., under review.

Bamber, D., 1975, The area above the Ordinal Dominance Graph and the area Below the Receiver Operating Characteristic Graph, Journal of Mathematical Psychology, 12, 387-415.

Brier, G. W., 1950, Verification of forecasts expressed in terms of probability, Mon. Wea. Rev., 78, 1-3.

Buizza, R., 1997: Potential forecast skill of ensemble prediction and spread and skill distributions of the ECMWF ensemble prediction system. Mon. Wea. Rev.,125, 99-119.

Chatfield, C., 2000: Time series forecasting. Chapman and Hall/CRC Press, p. 267.

Ehrendorfer, M., 1997: Predicting the uncertainty of numerical weather forecasts: A review. Meteorologische Zeitschrift, Neue Folge, 6, 147-183.

Hersbach, H., 2000: Decomposition of the continuous ranked probability score for ensemble prediction systems. Weather and Forecasting, 15, 559-570.

Houtekamer, P. L., L. Lefaivre, J. Derome, H. Ritchie, and H. L. Mitchell, 1996: A system simulation approach to ensemble prediction.Mon. Wea. Rev., Mon. Wea. Rev., 124, 1225-1242.

Leith, C. E., 1974: Theoretical skill of Monte-Carlo forecasts.Mon. Wea. Rev.,102, 409-418.

Mason, S. J., G. M. Mimmack, 2002: Comparison of Some Statistical Methods of Probabilistic Forecasting of ENSO. Journal of Climate: Vol. 15, No. 1, pp. 8-29. 

Molteni, F., and Buizza, R., 1999: Validation of the ECMWF Ensemble Prediction System using empirical orthogonal functions. Mon. Wea. Rev., 127, 2346-2358.

Molteni, F., R. Buizza, T. N. Palmer, and T. Petroliagis, 1996:The ECMWF ensemble system:Methodology and validation.Q. J. R. Meteorol. Soc., 122, 73-119.

Murphy, A. H., 1966: A note on the utility of probabilistic predictions and the probability score in the cost-loss ratio decision situation. J. Appl. Meteor., 5, 534-537. 

Murphy, A. H., 1973, A new vector partition of the probability score, J. Appl. Meteor., 12, 595-600.

Richardson, D. S., 2000: Skill and economic value of the ECMWF ensemble prediction system,

Q.J.R.Meteorol. Soc., 126, 649-668. 

Roulston, M. S., and L. Smith, 2002: Evaluating Probabilistic Forecasts Using Information Theory. Mon. Wea. Rev., 130, 1653-1660. 

Smith, L. A.,2000: Disentangling Uncertainty and Error: On the Predictability of Nonlinear Systems. In Nonlinear Dynamics and Statistics, ed. Alistair I. Mees, Boston, Birkhauser, 31--64.

Stanski, H. R., L. J. Wilson, and W. R. Burrows, 1989: Survey of common verification methods in meteorology. WMO World Weather Watch Technical Reprot No. 8, WMO/TD. No. 358.

Stevenson, D. B., and F. J. Doblas-Reyes, 2000: Statistical methods for interpreting Monte Carlo ensemble forecasts. Tellus, 52A, 300-322.

Talagrand, O., R. Vautard, and B. Strauss, 1998: Evaluation of probabilistic prediction systems. Proceedings of ECMWF Workshop on Predictability, 20-22 October 1997, 1-25.

Toth, Z., and E. Kalnay, 1997: Ensemble forecasting at NCEP and the breeding method.Mon.Wea. Rev, 125, 3297-3319.

Toth, Z., Y. Zhu, T. Marchok, S. Tracton, and E. Kalnay, 1998: Verification of the NCEP global ensemble forecasts. Preprints of the 12th Conference on Numerical Weather Prediction, 11-16 January 1998, Phoenix, Arizona, 286-289.

Wei, M., and Toth, Z., 2002: Ensemble perturbations and forecast errors. Mon. Wea. Rev., under review.

Zhu, Y., G. lyengar, Z. Toth, M. S. Tracton, and T. Marchok, 1996: Objective evaluation ofthe NCEP global ensemble forecasting system. Preprints of the 15th AMS Conference on Weather Analysis and Forecasting, 19-23 August 1996, Norfolk, Virginia, p. J79-J82.

FIGURE CAPTIONS

Figure 7.1. A hypothetical forecast probability density function p(x) (full curve) for a one-dimensional variable x, along with a verifying observed value x_o for a single case. The additional two curves represent possible distributions for the verifying values observed over a large number of cases when p(x) was forecast by two probabilistic forecast systems. The distribution p₁(x) (dash-dotted curve) is close to the forecast distribution p(x), while the distribution p₂(x) (dashed curve) is distinctly different from p(x) (see text for discussion).

Figure 7.2. Reliability diagram for the NCEP Ensemble Forecast System (see text for the definition of the event E under consideration). Full line: reliability curve for the operational forecasts. Dash-dotted line: reliability curve for perfect ensemble forecasts where 'observation' is defined as one of the ensemble members. The horizontal line shows the climatological frequency of the event E, p_c = 0.714. Insert in lower right: Sharpness graph (see text for details).

Figure 7.3. Brier Skill Score (BSS_c, full curve, positively oriented), and its reliability (B_Rel, short dash), and resolution (B_Res, dashed, both negatively oriented) components, as a function of forecast lead-time (days) for the ECMWF Ensemble Prediction System (see text for the definition of the event E under consideration). 

Figure 7.4. ROC curves for the same event and predictions as in Figure 3, for four different forecast ranges.

Figure 7.5. Information content as defined by Eq. 7.13 for calibrated probabilistic forcecasts (with near perfect reliability) based on a 10-member subset of the NCEP ensemble. Forecasts are made for 10 climatologically equally likely intervals for 500 hPa geopotential height values over the Northern Hemisphere extratropics (20-80 N), and are evaluated over the March-May 1997 period.

Figure 7.6. Root mean square error of 500 hPa geopotential height NCEP control (open circle), ensemble mean (full circle), and climate mean (full square) forecasts, along with ensemble spread (standard deviation of ensemble members around their mean, open square), as a function of lead time, computed for the Northern Hemisphere extratropics, averaged over December 2001 - February 2002.

Figure 7.7. Equal likelihood diagram, showing the percentage of time when the NCEP high (dashed) and equivalent resolution control (dash-dotted), and any one of the ten 0000 UTC perturbed ensemble 500 hPa geopotential height forecasts (dotted) verify best out of a 23-member ensemble (of which the other 11 members are initialized 12 hours earlier, at 1200 UTC), accumulated over grid-points in the Northern Hemisphere extratropics during December 2001 - February 2002. Chance expectation is 4.35 (solid).

Figure 7.8. Analysis rank histogram for a 10-member 0000 UTC NCEP ensemble of 500 hPa geopotential height forecasts over the Northern Hemisphere extratropics during December 2001 - February 2002.