ON THE ABILITY OF ENSEMBLES TO DISTINGUISH BETWEEN FORECASTS WITH

SMALL AND LARGE UNCERTAINTY

Zoltan Toth¹, Yuejian Zhu¹, and Timothy Marchok¹
National Centers for Environmental Prediction

Submitted to
Weather and Forecasting

May 11, 2000

¹General Sciences Corporation (Beltsville, MD) at NCEP

^{Corresponding author's address: Zoltan Toth, NCEP, Environmental Modeling Center, 5200 Auth Rd., Room 207, Camp Springs, MD 20746
e-mail: Zoltan.Toth@noaa.gov}

ABSTRACT

In the past decade ensemble forecasting has developed into an integral part of numerical weather prediction. It offers flow dependent forecast probability distributions, as compared to single value (or "control") forecasts, which are of more limited use. A unique aspect of an ensemble of forecasts that cannot be reproduced by a single control integration is its ability to distinguish between forecast cases with high and low uncertainty. This aspect of the NCEP ensemble is studied quantitatively by verifying the ensemble mode forecasts along with a traditional higher resolution control forecast, in terms of predicting 10 climatologically equally likely 500 hPa height intervals. A stratification of the forecast cases by the degree of overall agreement among the ensemble members reveals great differences in forecast performance between the cases identified by the ensemble as the least and most uncertain. This confirms that the ensemble forecast system is capable of identifying in advance the expected success rate of the forecasts. This is further demonstrated by two examples, where mean sea level pressure and probabilistic quantitative precipitation forecasts from the NCEP and ECMWF ensemble systems are studied and compared.

1. Introduction

During the past decade ensemble forecasting has become an integral part of Numerical Weather Prediction (NWP). Major meteorological centers now regularly produce and use ensemble forecasts (Molteni et al., 1996; Toth and Kalnay, 1993; Rennick, 1995; Houtekamer et al., 1996; Kobayashi et al., 1996). The provision of flow dependent forecast probability distributions of weather elements, that reveal the case dependent forecast uncertainty, has been considered as one of the main advantages of ensemble forecasting (Ehrendorfer, 1997).

The generation and verification of probabilistic forecasts based on ensembles was the subject of a number of recent studies (e. g., Anderson, 1996; Hamill and Colucci, 1997; Talagrand et al., 1998; Atger, 1999; Richardson, 2000). General statistics for the performance of the NCEP ensemble forecasting system were provided by Zhu et al. (1996, with a comparison to that of the ECMWF Ensemble Prediction System), and Toth et al. (1998, with a comparison to that of a single higher resolution control forecast). These earlier studies demonstrated that the ensemble forecasts can be used to generate skillful probabilistic forecasts, which, after a simple statistical postprocessing based on verification statistics from the recent past, become very reliable.

In recent studies (Mylne, 1999; Richardson, 2000; and Toth et al., 2000) it was also demonstrated that the potential economic value associated with the use of an ensemble forecasting system is considerably above that attainable by using a single, even higher resolution control forecast, given substantial uncertainty in the forecasts (i. e., 500 hPa height forecasts at and beyond 3 days). It was also shown (Toth et al., 1998) that the extra value associated with an ensemble of forecasts as compared to a single control forecast is due to two main factors: (1) the ensemble can provide a probability distribution that is more complete than a dichotomous probability description given by a single forecast; and (2) the ensemble can characterize foreseeable, flow dependent variations in the uncertainty of the forecasts. While the first factor (provision of a full probability distribution) could possibly be viewed as a formal and trivial one, the second factor (case dependent uncertainty estimates) is considered as providing genuine information that can be derived in practice only from an ensemble (Ehrendorfer, 1997). As it turns out, even full probabilistic forecast distributions based on a single control forecast cannot reach the skill level of that provided by an ensemble of forecasts (Talagrand, 1999, personal communication), attesting to the value of case dependent uncertainty information provided by the ensemble.

In this paper we investigate the practical question of how sharply an ensemble of forecasts, based on their flow dependent level of similarity or dissimilarity, can distinguish between forecast situations with lower or higher than average expected uncertainty. Ensemble forecasts over a period of a season (section 2) will be evaluated by stratifying the cases according to the degree of ensemble forecast similarity (section 3). The main results will be presented in section 4, while section 5 provides two examples. The conclusion and discussion are given in sections 6 and 7 respectively.

2. Ensemble forecast data

In the present study, the NCEP operational global ensemble forecasts (Toth and Kalnay, 1997) will be evaluated over the period March - May 1997, with the aim of assessing how sharply the ensemble forecasts can distinguish in advance between cases of higher or lower than average uncertainty. The studied period is from a transition season that coincides with that of Toth et al. (1998). Predictability in a transition season is lower than in winter but higher than in summer. Therefore the results reported here for a spring season may be viewed as typical for the overall performance of the ensemble.

The NCEP global ensemble forecasts in 1997 consisted each day of 17 individual forecasts run out to 16 days lead time, of which 3 were control forecasts started from unperturbed analyses, and 14 were perturbed forecasts started from initial conditions where bred perturbations of the size of estimated analysis uncertainty were both added to, and subtracted from the control analyses at 0000 and 1200 UTC (Toth and Kalnay, 1997). In the present study, the 14 T62 resolution perturbed forecasts (10 from 0000 UTC, and 4 from 1200 UTC) are evaluated, along with the 0000 UTC MRF T126 high resolution control forecast that provides a reference level of skill.

500 hPa height forecast and analysis data will be used over the Northern Hemisphere (NH) extratropics (20N - 77.5N), on a 2.5 by 2.5 latitude-longitude grid. As in Zhu et al. (1996), and Toth et al. (1998), the forecast and verifying analysis data will be projected at each grid point into 10 climatologically equally probable intervals (Fig. 1). These intervals were defined on a monthly basis using the NCEP reanalysis data (Kalnay et al., 1996), and were subsequently linearly interpolated for each date within the studied period.

3. Methodology

a. Stratification by expected uncertainty

On each day and at each grid point in the period and region studied, the distribution of the 14 ensemble forecasts at each lead time is evaluated in terms of the 10 climatologically equally likely bins. In particular, the number of ensemble forecast members associated with the most populous climate bin is noted. The most populous bin is the mode of the ensemble distribution and its value for a 14-member ensemble given in 10 climatologically equally likely bins varies between 2 and 14. High ensemble mode values (14, or close to 14) correspond to a compact ensemble, where most members indicate very similar height values, whereas low ensemble mode values (2, or close to 2) indicate a diverse ensemble where there is little agreement among the members. The former cases represent forecast situations with a small ensemble spread, with relatively small forecast uncertainty, while the latter cases are characterized by large ensemble spread, indicating large forecast uncertainty (see two forecast distribution examples in Fig. 1).

To evaluate the typical resolution of the ensemble in the probability space, next 10-15% of the total number of cases (over all gridpoints and days) associated with the highest and lowest ensemble mode values are identified for all lead times. At short lead times when the ensemble spread is generally small, cases with the highest ensemble mode (values close or equal to 14) capture 10-15% of all cases while at longer lead times more lower ensemble mode values need to be also included. As for the cases with the lowest ensemble mode, at long lead time values of 2 or slightly higher will account for 10-15% of all cases, due to the generally large ensemble spread. At shorter lead times with smaller ensemble spread, however, more higher mode values need to be also included to account for approximately the same fraction (10-15%) of all cases.

b. Measure of performance

The 10-15% of cases with the highest and lowest ensemble mode values will be referred to as the "small uncertainty" (or high predictability), and "large uncertainty" (or low predictability) cases respectively. This information on expected forecast uncertainty can be made available in real time to the forecasters when the ensemble forecast is released. The main results of this study shown in the next section pertain to the performance of ensemble mode forecasts, evaluated separately for the high and the low predictability cases. In addition, the average performance of the control MRF forecasts, which cannot be objectively classified into high or low predictability cases without information from the ensemble, will also be evaluated. The performance measure used for evaluating both the ensemble mode and MRF control forecasts is the average hit (or success) rate of the particular forecast system:

where h_f is the number of cases (hits) when a forecast system, calling for the occurence of a particular climate bin, correctly verified, and t_f is the total number of all such forecasts, accumulated over all climate bins. In section 4 hit rate results for the MRF control forecast (averaged over all cases), and for ensemble mode forecasts¹ evaluated separately over the high and low predictability cases, will be shown.

c. Attributes of probabilistic forecasts

The two main attributes of probabilistic forecasts are their reliability and resolution (see, e. g., Stanski et al., 1989). Reliability implies that forecast probability values match the conditional observed frequencies of the same events over the long run, e. g., forecasts issued with a 40% probability verify 40% of the time. Reliability, however, does not necessarily imply value. For example, if the climate probability of the predicted event is also 40%, the forecast would not have value with respect to using climatological information only. Resolution is a measure of how "sharp" the probabilistic forecasts are, i. e., how close the forecast probability values are to the ideal 0 and 1 values. Perfect resolution (i. e., the exclusive use of 0 and 1 probability values, as with the use of a single control forecast) does not guarantee optimal forecasts either, unless accompanied by perfect reliability. An ideal probabilistic forecast system in fact has as much resolution as possible, while exhibiting perfect reliability at the same time.

We know from earlier verification studies (e. g., Zhu et al., 1996; Toth et al., 1998) that probabilistic forecasts based on an ensemble (or a control forecast) can be easily calibrated, i. e., probability values based on the relative frequency of ensemble members indicating a particular weather event (here, one of the 10 climatologically equally likely bins) can be adjusted to match observed frequencies over the long run. This is because the system generally behaves consistently in time and the forecast probability values can just be relabeled to match the observed frequencies². In this study we assume that the ensemble based probabilistic forecasts can be perfectly calibrated, and explore how much resolution the forecasts have.

4. Results

Fig. 2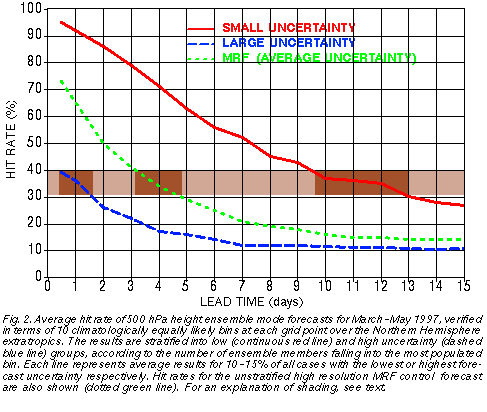 evaluates how different the hit rates of the forecasts are for the 10-15% of all cases with the lowest and the highest predictability, as identified in real time by the ensemble, as a function of lead time. The average hit rate for all cases, using the unstratified MRF forecasts, is also shown. Note that the ensemble mode forecasts evaluated for all cases without stratification (not shown) exhibit hit rates similar to that of the high resolution control, except with somewhat lower values before, and somewhat higher values after day 6 lead time (see Fig. 3 of Toth et al., 1998).

The results indicate that the ensemble forecasting system that was operational in the spring of 1997 had a substantial resolution. For example, at 1 day lead time the 10-15% of most predictable forecasts verified with a hit rate of 92%, while the least predictable 10-15% verified with a hit rate of only 36%. The average hit rate for the unstratified MRF forecasts was 65%. The verification statistics at later lead times reveal a somewhat reduced, but still wide range of hit rates. While the overall MRF hit rates at 4 (12) day lead time are 34% (15%), the most and least predictable 10-15% of the cases exhibit hit rates of 71% and 17% (35% and 11%) respectively. We should keep in mind that a fewer number of less frequently occuring cases with extremely low or high predictability would be associated with verification statistics even more anomalous than those presented in Fig. 2.

Note that the overall average hit rates (MRF control, dotted green line in Fig. 2) are closer to the stratified small uncertainty hit rates at very short lead time (cf. continuous red line at 12-hour), and to the large uncertainty hit rates at longer lead times (cf. dashed blue line at longer lead time). The skewness of the hit rate distribution is especially prominent at 10-day and longer lead times, suggesting that most of these forecasts are of poor quality, with a fewer number of exceptionally good forecasts.

Beyond exploring the large differences in verification statistics between the most and least uncertain cases at any given lead time, it is also interesting to compare at what lead time forecasts with different levels of uncertainty in Fig. 2 assume the same level of skill. Looking at the range of 0.3-0.4 hit rate values highlighted in Fig. 2, we can see for example that the least predictable 10-15% of the 1-day forecasts have a hit rate (36%) that is just about the same as the hit rate of 4-day MRF forecasts (34%, average predictability), or the hit rate of the most predictable 10-15% of the 12-day forecasts (35%).

5. Synoptic examples

In this section we present two synoptic examples to demonstrate the dramatic variations in the performance of NWP forecasts that can be objectively identified and foreseen with the use of an ensemble forecast system. Guidance on above or below average probabilistic ensemble mode forecasts is not routinely available yet. Operationally accessible ensemble spread forecasts, however, can also be used to identify cases with higher or lower than average predictability. In the two examples that follow mean sea level pressure and probabilistic quantitative precipitation forecasts will be considered.

a. Low uncertainty at long lead time

First we consider a deep low pressure system that developed in the Gulf of Alaska, affecting the US and Canadian west coast around 1200 UTC February 6, 1999. The analyzed mean sea level central pressure of the system had a closed contour of 968 hPa (Fig. 3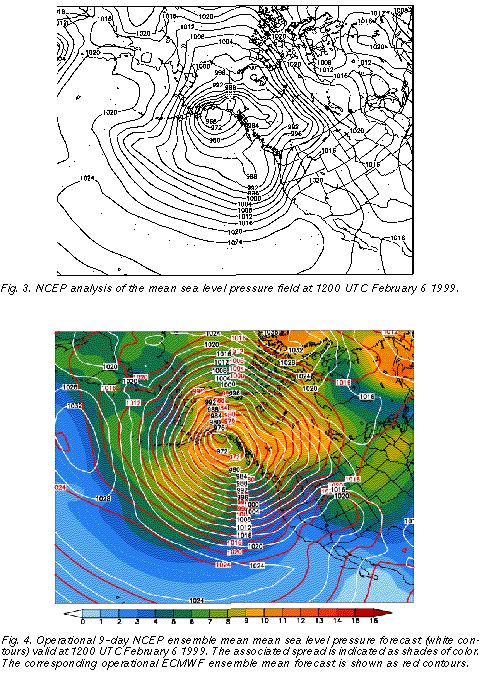), indicating a strongly anomalous flow with a 40 hPa negative anomaly from the long term mean. This cyclone was apparently associated with a very high degree of predictability. It was at 11.5 day lead time when the feature of the anomalous low was first noted in real time using the NCEP ensemble forecasts. And the ensemble mean of the mean sea level pressure forecast did not change much after the initial time of 0000 UTC January 27 (10.5 days lead time), with the deepest closed isobar of the low predicted between 972 and 964 hPa at 9.5 days and shorter lead times.

As an example, in Fig. 4 we present the 9 day NCEP ensemble mean forecast (white contours), along with its associated spread (shades of color). Over large areas of the storm and its environment, including the extreme central low pressure area, the associated ensemble spread (standard deviation of ensemble members around the mean) remained around or below 6 hPa. This is half or less than half of the average ensemble spread computed for the preceding month at this lead time (not shown), indicating well below average forecast uncertainty. The low level of forecast uncertainty is corroborated by the fact that consecutive ensemble mean and spread forecasts valid at the same time (not shown) were very similar. The greatly below average uncertainty for the studied case was further confirmed by a comparison of the NCEP and ECMWF (Molteni et al., 1996) ensemble mean forecasts, which were very similar again over a large area of the cyclone (cf. white and red contours in Fig. 4). A comparison of the 9 day ensemble mean forecast (Fig. 4) with the verifying analysis (Fig. 3) reveals that the forecasts for this cyclone, as expected from the real time uncertainty estimates, verified very well - the error in the central pressure forecasts was only a few hPa.

Comparing the large scale flow configurations at 12-hour (Fig. 5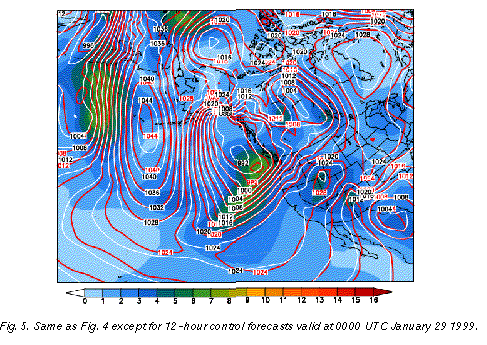) and 9-day (Fig. 4) lead time it is clear that the forecasts were not trivially persisting the observed features present around initial time. Great changes from extremely high to extremely low anomalous pressure conditions were predicted well over large areas, with changes from initial to final state reaching up to 40 hPa over Alaska and nearby areas. Note that the extremely low height values analyzed in Fig. 3 were well predicted by the ensemble mean forecasts (Fig. 4), documenting that the ensemble mean can retain highly anomalous flow patterns as long as these features are highly predictable.

It is interesting to note that analyzed 500 hPa height values near the center of the storm were around 4777 m with a negative anomaly of more than 500 m, falling into the lowest 1% of historical cases based on the NCEP/NCAR reanalysis. At 9-day lead time, 80% (40%) of all ensemble members fell into the lowest 2% (1%) of the climatological distribution, giving a strong indication for the possible occurence of extreme low values.

The low ensemble spread in Fig. 4 indicates that all members were rather similar. Therefore it is not surprising that the MRF control forecast also verified well. A user with access to only a single control forecast, however, could not have made much use of a control forecast on its own. Given the low levels of average skill at the 9-11 day lead time (less than 20% hit rate, see dotted green curve in Fig. 2), forecasts would be issued with a very low level of confidence, that would render them useless for a wide range of users (see, e. g., Fig. 4 of Toth et al., 2000). Yet with access to information on the widely varying levels of uncertainty, indicated reliably by the ensemble, there are times when weather forecasts with much increased confidence can be made (cf. lightly hatched distribution in Fig. 1, and continuous red curve in Fig. 2).

The above case provides such an example, where confident extended range daily sensible weather forecasts could have been issued based on the ensemble guidance. For example, 12 or more of the 17-member NCEP ensemble forecsts (70-100%) indicated a half inch or more 24-hour accumulated precipitation at 10-day and shorter lead times³ (Fig. 6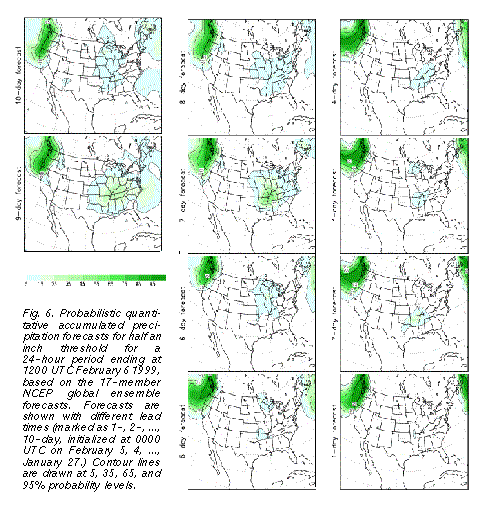) over all areas on the northwest coast that actually recieved that much precipitation. Similarly, at 7-day or shorter lead times, the ensemble predicted 70% or higher probabilities for most areas affected by more than an inch of precipitation (Fig. 7b). 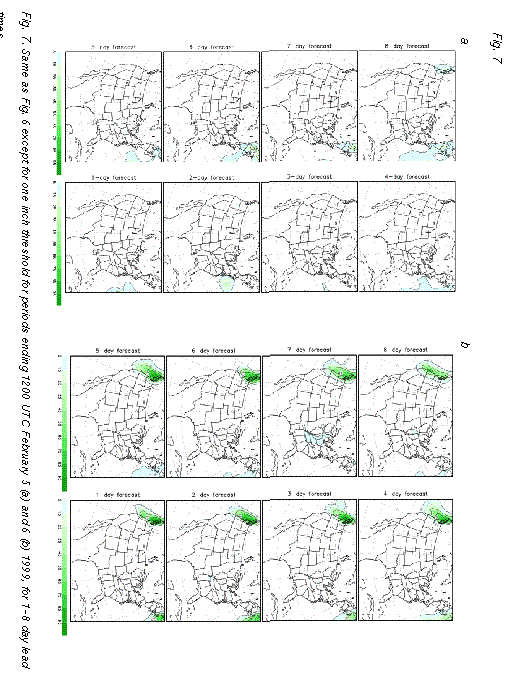We note that the time development of the weather associated with the storm, as suggested by the unusually low ensemble spread over large areas surrounding the storm, was also well predicted. For example, in contrast to the 70% and higher forecast probability of an inch or more precipitation corresponding to the observed precipitation event around 0000 UTC February 6, the ensemble correctly gave zero probability at 7-day and shorter lead times for more than an inch of precipitation for the preceding 24-hour period, centered around 0000 UTC February 5 (Fig. 7a).

b. High uncertainty at short lead time

The previous example illustrated the potential value of the ensemble approach in identifying weather features associated with low forecast uncertainty, even at long lead times. In this subsection an example is shown for identifying cases with unusually high forecast uncertainty. Identifying these cases can be especially valuable at shorter lead times where the overall level of forecast skill is relatively high. Interestingly, a prominent example of this kind offers itself in the same forecast studied in Fig. 4, but valid at a very short lead time.

Shown in Fig. 5 is the 12-hour lead time NCEP high resolution control forecast (called "AVN", white contours), valid at 0000 UTC January 29 1999. A closed low, associated with a cold front extending to the southwest, is seen over the eastern Pacific approaching the west coast of the US. The ensemble spread associated with this system is around 6 hPa. This is the same level of uncertainty found over large areas of the storm studied in the 9-day forecast example of Fig. 4. But while the 6 hPa spread is half or less of the usual spread at 9 days lead time (Fig. 4), it is up to 3 times more than the usual spread at the 12-hour lead time (Fig. 5).

A comparison of the 12-hour NCEP control forecast to that from ECMWF (cf. white and red contours in Fig. 5) confirms the unusually large degree of uncertainty regarding the position of the closed low. The largest differences between the two fields, which reach up to 5 hPa, occur in the area of large ensemble spread. The 5 hPa difference observed between the two control forecasts over the eastern Pacific low pressure system at 12-hour lead time (Fig. 5) is actually above the level of difference present between the two ensemble mean forecasts 8.5 days later, near the center of the Gulf of Alaska storm where the differences are 4 hPa or less (Fig. 4).

Given the high level of average success rate of 12-hour forecasts (65%, see dotted green curve on Fig. 2), a weather forecast based on a single control integration in this case may provide misleading guidance in terms of overconfidence. Information again from the ensemble, in this case about larger than normal spread, can provide case dependent uncertainty estimates (see the heavily hatched distribution in Fig. 1, and the dashed blue curve in Fig. 2) which can be crucial in many applications.

The large 12-hour lead time forecast differences present within the NCEP ensemble, and between the ECMWF and NCEP control forecasts off the northwest US coast in Fig. 5 (around 6 hPa) would certainly be associated with different weather conditions, with the ECMWF forecast, for example, suggesting stronger onshore winds, associated with heavier precipitation. Note that the same northeast Pacific area in the 9-day forecast (Fig. 4) is associated with the same or lesser degree of uncertainty (5-6 hPa ensemble spread and forecast differences).

It is interesting to note that based on the results of Fig. 2, 10-15% of the time a 9-day forecast is expected to be more accurate than 12-hour forecasts on the least predictable 10-15% of cases. It follows that the chances that both a large uncertainty 12-hour forecast and a small uncertainty 9-day forecast would appear on the same day and in the same area is on the order of 1-2%. In other words, in an average year and at any location 4-6 days are expected when a 9-day forecast can be made with the same or slightly higher certainty than a 12-hour forecast. As a reference, both of these forecasts would exhibit a skill of the level of an average 3-day forecast.

6. Conclusion

The above analysis of the NCEP global ensemble forecast system was based on verification results of the ensemble mode and higher resolution control forecasts, the former stratified according to the value of the ensemble mode, which represents a measure of how tightly or loosely distributed the ensemble members are. The ensemble forecasts are found to possess a substantial amount of resolution in the probability space, and therefore can reliably indicate, at the time weather forecasts are prepared, the large case to case variations in forecast uncertainty. For example, 10-15% of the 1-day forecasts identified as the least and most uncertain by the NCEP ensemble have associated success rates of 92% and 36%; the same numbers for 4 (and 12) day forecasts are 71% and 17% (35% and 11%) respectively. The fact that 25% of all cases are affected by the results described above highlights the relevance of the ensemble approach to everyday weather forecasting. At any location and at any lead time both the low and high uncertainty cases in Fig. 2 are encountered, on average, once a week.

A further analysis of the results, along with those of other studies (see, e. g., Toth and Kalnay, 1995) suggests that on one hand, daily weather prediction for the 6 to 15 days range is possible in cases identified by the ensemble as highly predictable, with the same accuracy and confidence as that of short range forecasts with poorer than average predictability. As Fig. 4 examplifies, from time to time even extremely anomalous weather patterns can be forecast with high confidence in the extended range. On the other hand, in flow configurations with unusually low predictability, the skill of short range forecasts is expected to be as low as average medium-range, or above average extended range forecasts.

The large variations in forecast uncertainty revealed above are a function of (1) the size and distribution of errors in the analysis fields used to initialize NWP forecasts, and (2) the particular evolution of flow patterns from initial to final forecast times. Variations in forecast uncertainty are a direct consequence of the chaotic nature of the atmosphere and are out of the control of the forecasters. Before the advent of ensemble forecasting, forecasters had no or very limited advance knowledge of these changes in forecast uncertainty. With ensemble forecasting, as recent studies have demonstrated, these dramatic changes have become routinely predictable. How probabilistic information from the ensemble can be conveyed to, and used by forecasters and end users will be briefly discussed in the next section.

7. Discussion

a. Use of probabilistic ensemble mode forecasts

Both the ensemble mode and control forecasts evaluated in this paper are single value or categorical forecasts. The ensemble system, however, also provides case dependent uncertainty estimates. This additional information can make a substantial difference in terms of the utility of forecasts in real life decision making processes. The actual increase in information content due to the variations in forecast uncertainty foreseeable by the ensemble can be quantified. Toth et al. (1998) found that the ensemble mode forecast, which has roughly the same average hit rate as the high resolution control forecast, has 30-70% more information content in the 5-7 day lead time range, and 2-3 times more afterward, than the high resolution control, due to its ability to identify in advance cases with higher or lower than average predictability.

Based on these results NCEP plans to introduce geographical displays of case dependent probabilistic guidance associated with the ensemble mode forecast, in terms of the forecast probability of the most likely bin out of 10 climatologically equally likely intervals. Above and below average probability values at all lead times will be highlighted in different colors (corresponding to the hit rates for cases with high and low predictability, respectively in Fig. 2) for easy identification of areas with significant deviations from average forecast uncertainty.

b. Full forecast probability distributions

Beyond indicating the varying level of forecast uncertainty, the ensemble forecasts can also provide full forecast probability distributions, thus further increasing the potential economic value attainable from the use of weather forecasts. The generation and use of probability distributions, instead of single value (or categorical) forecasts requires a conceptual change on the part of the forecaster but this is a change necessary for realizing all the benefits an ensemble has to offer.

Consider, for example, users who are sensitive to sub-freezing temperatures. If a particular user incurs large losses in case he/she does not protect against freezing temperatures (low cost-loss ratio), he/she will want to know about the probability of freezing, and take action, even if freeezing is not the most likely forecast event. Providing a full forecast probability distribution will well serve the interests of all users. As noted earlier, such forecasts can be made by statistically postprocessing a single control forecast; however, the quality of these probabilistic forecasts remains below that based on an ensemble of forecasts (Talagrand, 1999, personal communication).

c. Utility of ensemble forecasts

Reliable, real-time information on variations in forecast uncertainty from an ensemble can make a large difference in the economic value of weather forecasts. For many potential users, the addition of such information may make the forecasts practically usable, as compared to relying strictly on climatological information (e. g., Toth et al., 2000). Let us consider again a user who is sensitive to subfreezing temperatures, but whose cost of protection is close to the losses he/she suffers if not protected (high cost-loss ratio). This user, unless supplied with very accurate forecasts, will choose, based on the climatological frequency of the harmful (subfreezing temperature) event to either always protect (in case the harmful event has a high climatological frequency), or never protect (low climatological frequency, see, e. g., Richardson, 2000). Beyond a very short lead time, the average hit rate of a control forecast drops dramatically (see dotted green curve in Fig. 2), and the users, in order to minimize their losses, have to resort to using climatological information.

Ensemble forecasts, however, can identify forecast cases when accurate forecasts can be made even at longer lead times. Users, who would never protect based on low climatological freezing temperature frequency, can benefit from this by altering their strategy and taking protective action when the freezing event is predicted with a low forecast uncertainty. Alternatively, in case of high climatological frequencies of freezing temperatures, users would skip taking protective action if, on a particular day, the occurence of non-freezing temperature is predicted with low uncertainty. In general, probabilistic forecasts based on an ensemble offer more potential economic value than even higher resolution single control forecasts. Even at short, 24-hour lead time, users with cost-loss ratios in the low or high range can benefit only from the probabilistic forecasts with case dependent uncertainty estimates, based on an ensemble (see Fig. 1 in Toth et al., 2000). And beyond 3-day lead time the ensemble offers more economic benefit for all users (Richardson, 2000; Mylne, 1999; Toth et al., 2000).

The performance of NWP forecasts, whether control or ensemble, are negatively affected by the use of imperfect forecast models. The hit rates reported in this study, for example, are lower than they would be under ideal conditions, due to simplifications in model formulation. The utility of ensemble forecasts is also limited by shortcomings in the formation of the ensemble. The NCEP ensemble, for example, accounts for forecast uncertainty related only to errors in initial conditions, but not to errors caused by model imperfectness. Therefore the range of foreseeable variations in forecast skill would be wider could we predict the occurence of flow dependent random or systematic model errors. The results in this and other studies evaluating operational ensemble forecasts naturally reflect all these limiting factors and represent the currently operationally attainable levels of skill. Under these limiting conditions, the ensembles exhibit great value beyond that of single control forecasts, and are ready to be used by forecasters and end users alike. The fact that the system is not perfect and can be improved in the future should not discourage anyone from taking full advantage of what ensemble forecasting can currently offer.

8. Acknowledgements

We are grateful to David Burridge, Director, and the staff of ECMWF, in particular Horst Boettger and John Henessy, for participating in an exchange of ensemble forecasts between ECMWF and NCEP on a research basis. Richard Wobus of GSC provided help with data processing. Steven Tracton, Ed O'lenic, and Peter Manousos of NCEP, and John Jacobson of GSC provided helpful comments on an earlier version of the manuscript.

9. References

Anderson, J. L., 1996: A method for producing and evaluating probabilistic forecasts from ensemble model integrations, J. Climate, 9, 1518-1530.

Atger, F., 1999. The skill of ensemble prediction systems. Mon. Wea. Rev., 127, 1941-1953.

Ehrendorfer, M., 1997: Predicting the uncertainty of numerical weather forecasts: A review. Meteorologische Zeitschrift, Neue Folge, 6, 147-183.

Hamill, T. M., and S. J. Colucci, 1997: Verification of Eta-RSM short-range ensemble forecasts. Mon. Wea. Rev., 126, 711-724.

Houtekamer, P. L., L. Lefaivre, J. Derome, H. Ritchie, and H. L. Mitchell, 1996: A system simulation approach to ensemble prediction. Mon. Wea. Rev., 124, 1225-1242.

Kalnay, E., M. Kanamitsu, R. Kistler, W. Collins, D. Deaven, L. Gandin, M. Iredell, S. Saha, G. White, J. Woollen, Y. Zhu, M. Chelliah, W. Ebisuzaki, W. Higgins, J. Janowiak, K. C. Mo, C. Ropelewski, J. Wang, A. Leetmaa, R. Reynolds, Roy Jenne, and Dennis Joseph, 1996: The NMC/NCAR 40-Year Reanalysis Project". Bull. Amer. Meteor. Soc., 77, 437-471.

Kobayashi, C., K. Yoshimatsu, S. Maeda, and K. Takano, 1996: Dynamical one-month forecasting at JMA. Preprints of the 11th AMS Conference on Numerical Weather Prediction, Aug. 19-23, 1996, Norfolk, Virginia, 13-14.

Molteni, F., R. Buizza, T. N. Palmer, and T. Petroliagis, 1996: The ECMWF ensemble system: Methodology and validation. Q. J. R. Meteorol. Soc., 122, 73-119.

Mylne, K.R., 1999 The use of forecast value calculations for optimal decision making using probability forecasts. Preprints of the 17th AMS Conference on Weather Analysis and Forecasting, 13-17 September 1999, Denver, Colorado, 235-239.

Rennick, M. A., 1995: The ensemble forecast system (EFS). Models Department Technical Note 2-95, Fleet Numerical Meteorology and Oceanography Center. p. 19. [Available from: Models Department, FLENUMMETOCCEN, 7 Grace Hopper Ave.,Monterey, CA 93943.]

Richardson, D. S., 2000: Skill and economic value of the ECMWF ensemble prediction system, Q.J.R.Meteorol. Soc., 126, 649-668.

Stanski, H. R., L. J. Wilson, and W. R. Burrows, 1989: Survey of common verification methods in meteorology. WMO World Weather Watch Technical Reprot No. 8, WMO/TD. No. 358.

Talagrand, O., R. Vautard, and B. Strauss, 1998: Evaluation of probabilistic prediction systems. Proceedings of ECMWF Workshop on Predictability, 20-22 October 1997, 1-25.

Toth, Z., and E. Kalnay, 1993: Ensemble Forecasting at the N MC: The generation of perturbations. Bull. Amer. Meteorol. Soc., 74, 2317-2330.

Toth, Z., and E. Kalnay,1995: Ensemble forecasting at NCEP. Proceedings of the ECMWF Seminar on Predictability. September 4-8, 1995, Reading, England, p. 39-60.

Toth, Z., and E. Kalnay, 1997: Ensemble forecasting at NCEP and the breeding method. Mon. Wea. Rev, 125, 3297-3319.

Toth, Z., Y. Zhu, T. Marchok, S. Tracton, and E. Kalnay, 1998: Verification of the NCEP global ensemble forecasts. Preprints of the 12th Conference on Numerical Weather Prediction, 11-16 January 1998, Phoenix, Arizona, 286-289.

Toth, Z., Y. Zhu, and R. Wobus, 2000: On the economic value of ensemble based weather forecasts. Preprints of the 15th AMS Conference on Probability and Statistics in the Atmospheric Sciences, 8-11 May 2000, Ashville, NC, in print.

Zhu, Y., G. lyengar, Z. Toth, M. S. Tracton, and T. Marchok, 1996: Objective evaluation ofthe NCEP global ensemble forecasting system. Preprints of the 15th AMS Conference on Weather Analysis and Forecasting, 19-23 August 1996, Norfolk, Virginia, p. J79-J82.

2#. Such a procedure amounts to a bias removal in the probability space and is called calibration. For the generation of reliable probabilistic forecasts calibration is a necessary step because neither the model, nor the generation of the ensemble is perfect. For example, in most cases ensemble forecasts have insufficient spread.

3#. The high degree of predictability in terms of accumulated precipitation is apparently related to the fact that in this case the precipitation is partly orographically forced.