ON THE ECONOMIC VALUE OF ENSEMBLE BASED WEATHER FORECASTS
Zoltan Toth1, Yuejian Zhu1, and Richard Wobus1
National Centers for Environmental Prediction
Submitted to the
Bulletin of American Meteorological Society
May 3, 2000
1General Sciences Corporation (Beltsville, MD) at NCEP
Corresponding author's address: Zoltan Toth, NCEP, Environmental Modeling Center, 5200 Auth Rd., Room 207, Camp Springs, MD 20746
e-mail: Zoltan.Toth@noaa.gov
ABSTRACT
The potential economic benefit associated with the use of an ensemble of forecasts
vs. an equivalent or higher resolution control forecast is discussed. A simple decision
making model is used where all potential users of weather forecasts are characterized by
the ratio between the cost of their action to prevent weather related damages, and the loss
that they incur in case they do not protect their operations. It is shown that in cases of
appreciable forecast uncertainty the ensemble forecast system can be used by a much
wider range of users, and with significantly greater overall potential economic benefits,
than a control forecast, even if the latter is run at a higher resolution. It is argued that the
added benefits derive from (1) the ensemble's ability to differentiate between high and low
predictability cases, and (2) the fact that it provides a full forecast probability distribution,
allowing the users to tailor their weather forecast related actions to their particular cost/loss
situation.
1. Introduction
During the past decade, due to increased computer resources, the development of
more realistic atmospheric models, and the recognition of the importance of atmospheric
predictability in general, ensemble forecasting became a major component of Numerical
Weather Prediction (NWP). NWP centers around the globe (European Center for Medium
Range Weather Forecasts, Molteni et al., 1996; the National Centers for Environmental
Prediction, Toth and Kalany, 1993; the Canadian Meteorological Center, Houtekamer et al.,
1996; the Fleet Numerical Oceanographic and Meteorlogical Center, Rennick et al., 1995;
the Japan Meteorological Agency, Kobayashi et al., 1996; and the South African Weather
Bureau, Tennant, 1998, personal communication) started to produce operational
ensemble forecasts, where the models are integrated a number of times, started from
slightly perturbed initial conditions, in addition to generating the traditional "control"
forecast, started from the best available atmospheric analysis. Through the ensemble
approach one can generate probabilistic forecasts for assessing the case dependent
forecast uncertainty related to small errors in the initial conditions and the models used.
When new forecast techniques emerge, some questions naturally arise: Does the
new method provide guidance that is of higher quality or more use than existing methods?
Is the potential benefit from running a new technique cost effective? Is the new method
sufficient with respect to old methods (Ehrendorfer and Murphy, 1988), i. e., is using the old
technique redundant, given the new guidance? These are questions that should be
addressed with respect to using the relatively new ensemble technique, as compared to
relying on the use of a traditional single control forecast.
In earlier studies we presented a detailed analysis of the quality of probabilistic
forecasts generated based on the NCEP ensemble forecasting system (Toth and Kalnay,
1997). The performance of the NCEP ensemble forecasts was also compared to that of the
ECMWF ensemble prediction system (Zhu et al., 1996), and a single higher resolution
MRF control forecast (Toth et al., 1998). These earlier studies give valuable insight into the
behavior of the different forecast systems, thus providing feedback to the developers.
Nevertheless, the ultimate measure of the utility of weather forecasts is arguably the
economic benefit associated with their actual use in the daily decision making process of
individuals or different organizations.
Simplistically, users of weather forecasts either do, or do not take action (e. g.,
introduce protective action to prevent/reduce weather-related loss), depending on
whether a particular weather event is forecast or not. Cost-loss analysis of different
complexity can be applied to evaluate the economic impact of the use of weather forecasts
on the users (Murphy, 1985; Katz and Murphy, 1997). Studies of the economic value of
weather forecasts can either be descriptive, assessing the value of forecasts used, often
suboptimally, by existing customers; or prescriptive, identifying the potential value of
forecasts, assuming they are used in an optimum manner (Stewart, 1997).
In this paper we evaluate the potential economic value associated with the use of an
ensemble of forecasts, vs. an equivalent, and a higher resolution control forecast, using a
relatively simple cost-loss model discussed previously by Richardson (2000a) and Mylne
(1999). The cost-loss analysis approach followed in this study obviously has its limitations.
For example, not all values can be expressed in terms of dollar amounts; the loss of life is
one such example. Nevertheless the economic analysis used offers a framework that, after
some simplifications, can generally be applied in most cases.
2. Cost-loss analysis
A decision maker becomes a user of weather forecasts if he/she alters his/her
actions based on forecast information. If, based upon a particular weather forecast, a user
takes a preventive action, and the predicted harmful event does not occur (false alarm, FA),
the user incurs a cost (C) associated with his/her action (Table 1)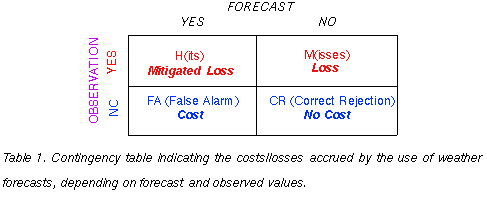 . In a case where the event
is not forecast the user does not take action, and if the event does not occur (correct
rejection, CR), there is no cost (N) on the part of the user. If an event is not forecast but
occurs (missed event, M), the user is not protected and suffers a loss (L>C). When,
following the forecast of a harmful event a user takes protective action and the event occurs
(hit, H), the user has to pay the cost of his action (C), plus may still incur some reduced loss,
with a total cost called mitigated loss (ML; typically, C<ML<L).
. In a case where the event
is not forecast the user does not take action, and if the event does not occur (correct
rejection, CR), there is no cost (N) on the part of the user. If an event is not forecast but
occurs (missed event, M), the user is not protected and suffers a loss (L>C). When,
following the forecast of a harmful event a user takes protective action and the event occurs
(hit, H), the user has to pay the cost of his action (C), plus may still incur some reduced loss,
with a total cost called mitigated loss (ML; typically, C<ML<L).
a. Mean expense
If the relative frequency of the four different outcomes in Table 1 (H, FA, CR, and M)
is known and marked by h, fa, cr, and m, one can assess, in a statistical sense, the mean
expense (ME) of a user of a forecast system:
MEfc=hML+mL+faC (+crN). (1)
Furthermore, one can determine the mean expense associated with using climatological
information only:
MEcl=min[oL, oML+(1-o)C], (2)
where o is the climatological frequency of the event. Based on the climatological frequency
of the event and on the user's associated costs and losses, the user will either always or
never take protective action. A decision maker will choose to use a forecast system if
his/her mean expense associated with the forecast system will be lower than that
associated with using only climatological information.
b. Economic value
The minimum expense for a user, given a perfect forecast system that provides
accurate predictions for the occurence and non-occurence of a particular event, can be
written as:
MEperf=oML. (3)
In this ideal situation, the user takes protective action if and only if a harmful event actually
occurs. Using Eqs. (1-3) the definition of the relative economic value (V) of a forecast
system can be given as

Using a forecast system that is perfect will result in an economic value of 1 (maximum
value), while a forecast system associated with the mean expense equal to (larger than)
that attainable using climatological information only will have zero (negative) economic
value.
Substituting Eqs. (1-3) into Eq. 4 we arrive at
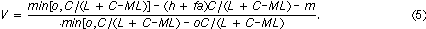
By recognizing that the actual loss which is protected by taking action is L+C-ML (La, see
Richardson, 2000a), Eq. 5 can be written as:
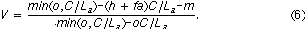
In the special case the users, by their protective action, can perfectly shield themselves
from the adverse effect of weather, the mitigated loss is equal to the cost of the protective
action (ML=C), and La=L.
As shown by, e. g. Mylne (1999), the economic value defined above is related to the
Relative Operating Characteristics (ROC, see, e. g., Mason, 1982), a signal detection
theory based measure of forecast performance. On an ROC plot the hit rate HR=H/(H+M)
is plotted against the false alarm rate FR=FA/(FA+CR) of a forecast system and its overall
performance is measured by the ROC-area defined by the points (0,0), (1,1), and the
point(s) representing the forecast system (see, eg., Stanski et al., 1989). Note that the
economic value of forecasts (V) depends only on two forecast performance parameters (h
and m in Eq. 5), which can be also expressed by HR and FR used in the definition of ROC.
Not surprisingly the overall economic value of a forecast system and the ROC-area and
Brier Skill Score measures (BSS, which is a measure related to ROC-area for systems with
forecast probabilities exactly matching observed frequencies, Talagrand et al., 1998) are
closely related (Richardson, 2000b). For example, BSS measures the overall economic
value associated with a particular forecast system, assuming that when all users are
considered, the same amount of property is at stake at each cost-loss ratio value (Murphy,
1966).
Beyond the parameters describing the forecast system, V also depends on o, the
climatological frequency of the event, and on C/La, the cost-loss ratio that depends on the
particular user of a forecast system. The fact that all users can be characterized in this
framework by a single variable, C/La, offers a convenient way to evaluate the potential
economic value of any forecast system for all users on a two-dimensional, V vs. C/La or
La/C plot.
3. Experimental setup
In the following section we compare the economic value of the MRF T62 and T126
resolution control forecasts to that of a 14-member set of the T62 horizontal resolution
NCEP ensemble for the April - June 1999 period. Note that the computational cost of
generating either a higher, T126 resolution control forecast, or a 14-member T62
resolution ensemble is an order of magnitude higher than running a T62 resolution control
forecast only. In the example below, weather events are defined as the 500 hPa
geopotential height at gridpoints over the Northern Hamisphere extratropics being in any of
10 climatologically equally likely bins (Toth et al., 2000).
Deterministic guidance from a single forecast can be unambiguously interpreted by
a user. If a particular adverse weather event is forecast, the user can take protective action,
and do nothing otherwise. In case of an ensemble of N forecasts, the user has N options.
He/she can choose to take action only if all N forecasts predict the adverse weather, act if
N-1, N-2, ..., or even if only 1 member predicts the adverse weather. Each of these
decision criteria corresponds with a different economic value. Based on their C/La ratio,
users can choose the decision criterion that offers the most value to them. In fact, it can be
shown that the best decision level p, corresponding to the predicted probability of the
weather event, is equal to C/La (Murphy, 1977). The higher the cost of the protective action
relative to the potential loss, the more certainty the user requires about the forecast before
he/she takes action. One of the potential advantages of using an ensemble forecast
system is that it naturally provides a multitude of such decision criteria. Different users can
then tailor their use of the forecast information to their particular application, characterized
by their cost-loss ratio.
Relative frequency values based on counting how many ensemble members
predict a certain event usually provide probabilistic forecasts that are biased in a sense that
they do not necessarily match corresponding observed frequency values. This is because
of deficiencies in model and ensemble formulation. For example, when half of the
ensemble members predict a weather event, that event may, over a long verification
period, verify only 40% of the time. Such biases in ensemble-based probabilities are
generally consisitent in time and can be easily eliminated (see, e. g., Zhu et al., 1996). The
calibrated forecast that would be issued based on the past verification statistics in the
above case, where half of the ensemble members predict an event, for example, is 40%.
The April - June 1999 ensemble based probabilistic forecasts evaluated in this paper have
been calibrated using independent data from February 1999 verification statistics. For
each loss-cost ratio shown in Figs. 1-4 the decision criterion for the ensemble is based on
the calibrated probability forecasts. In particular, it is assumed that a user will take
protective action if the calibrated probability forecast value is greater or equal to the
cost-loss ratio (p>C/La). For the extremely high (and low) probablity values where the finite
ensemble cannot provide optimum guidance, the best available guidance was used, i. e.,
the highest (lowest) probability values associated with all (only one) members predicting
the weather event. The above decision making algorithm, based on the users' cost-loss
ratio and the calibrated probability forecasts, represents an operationally feasible optimum
strategy for the use of ensemble guidance.
As noted above, a single control forecast provides a unambiguous signal whether to
protect against adverse weather or not. Therefore, unlike in the case of the ensemble
forecasts, the users' response cannot be optimized through calibration of probabilistic
guidance.
4. Results
In Fig. 1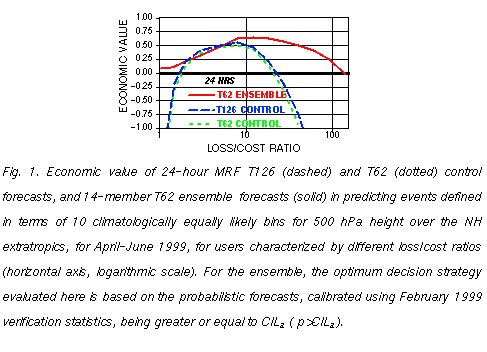 we show the economic value of the two control forecasts vs. an ensemble of
forecasts at 24-hour lead time, as a function of the La/C ratio, as discussed above. The
economic value comparison results indicate that even at this short, 24-hour lead time, for
this well predictable variable, most potential users, except those with loss-cost ratios in a
relatively narrow band between 2 and 5, can realize more economic value when using the
ensemble forecasts. At and beyond 72 hours lead time (Figs. 2-4)
we show the economic value of the two control forecasts vs. an ensemble of
forecasts at 24-hour lead time, as a function of the La/C ratio, as discussed above. The
economic value comparison results indicate that even at this short, 24-hour lead time, for
this well predictable variable, most potential users, except those with loss-cost ratios in a
relatively narrow band between 2 and 5, can realize more economic value when using the
ensemble forecasts. At and beyond 72 hours lead time (Figs. 2-4)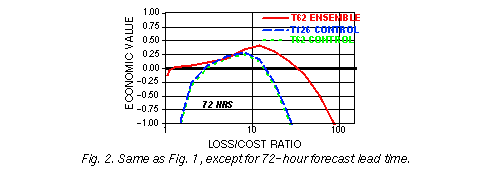
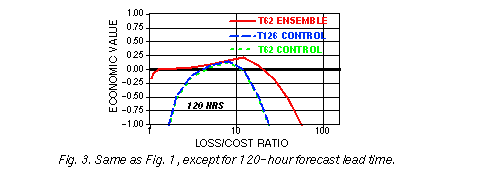
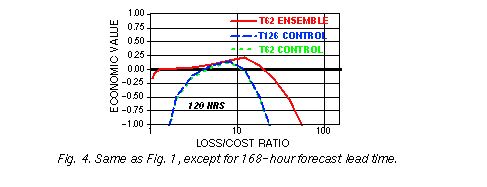 virtually all users are
better off using the ensemble system than the control forecasts. Furthermore, the range of
loss-cost ratios for which the forecasts exhibit value, compared to using climatological
information only, is substantially widened, indicating that a much larger group of users can
benefit from the ensemble forecasts as compared to the control forecasts. Note that on
each of the figures the largest economic benefit is, as expected theoretically (see, e. g.,
Richardson, 2000a), attained by users whose C/La ratio is approximately equal to o, the
climatological frequency of the weather event, which in our case is 0.1. Note also that with
increasing lead time the economic value, as compared to using perfect forecasts, just as
the forecast information content (see Fig. 8 of Toth et al., 1998), is reduced.
virtually all users are
better off using the ensemble system than the control forecasts. Furthermore, the range of
loss-cost ratios for which the forecasts exhibit value, compared to using climatological
information only, is substantially widened, indicating that a much larger group of users can
benefit from the ensemble forecasts as compared to the control forecasts. Note that on
each of the figures the largest economic benefit is, as expected theoretically (see, e. g.,
Richardson, 2000a), attained by users whose C/La ratio is approximately equal to o, the
climatological frequency of the weather event, which in our case is 0.1. Note also that with
increasing lead time the economic value, as compared to using perfect forecasts, just as
the forecast information content (see Fig. 8 of Toth et al., 1998), is reduced.
To summarize the results, in Fig. 5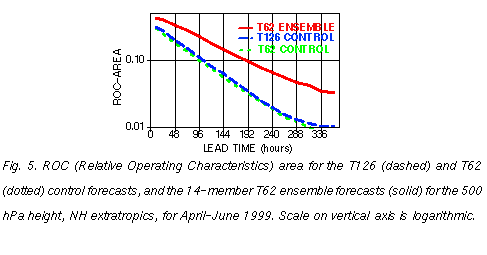 we show the ROC-area scores for the T62 and
T126 control, and the T62 ensemble forecast systems, for different lead times. Recall that
the ROC-area can be considered as a summary measure of overall economic value of the
forecasts (Richardson, 2000b). The exact implicit assumption in the ROC-area
calculations about the distribution of value protected by different users with respect to their
cost-loss ratio is not known. Unfortunately, little if any information is available on most
users' cost-loss ratio either. Nevertheless Fig. 5 can provide an indication for the overall
utility of the three forecast systems. Perfect (climatological) forecasts correspond to a
value of 0.5 (0) ROC area, while negative values indicate economic loss compared to using
climatological guidance.
we show the ROC-area scores for the T62 and
T126 control, and the T62 ensemble forecast systems, for different lead times. Recall that
the ROC-area can be considered as a summary measure of overall economic value of the
forecasts (Richardson, 2000b). The exact implicit assumption in the ROC-area
calculations about the distribution of value protected by different users with respect to their
cost-loss ratio is not known. Unfortunately, little if any information is available on most
users' cost-loss ratio either. Nevertheless Fig. 5 can provide an indication for the overall
utility of the three forecast systems. Perfect (climatological) forecasts correspond to a
value of 0.5 (0) ROC area, while negative values indicate economic loss compared to using
climatological guidance.
The ensemble forecast system is found to outperform the control forecasts at all
lead times. For example, at day 2 (6) lead time the use of the ensemble forecast system
provides close to 70% (130%) more overall economic benefit than the control forecasts; to
put it in another way, a 4-day (10-day) ensemble forecast offers as much value as a 2-day
(6-day) single control forecast. Similarly, the use of a 6-day ensemble forecast offers
130% more economic value than a 6-day control forecast; and the same level of value can
be attained by the use of a 10-day ensemble forecast. These results are in good
agreement with Figs. 1-4, and at later lead time with those of Mylne (1999) and Richardson
(2000a).
Over the Northern Hemisphere extratropics the T126 resolution version of the
NCEP MRF model generally exhibits higher skill scores than, and is considered to be
superior to the T62 resolution model version (P. Caplan, 1999, personal communication).
Nevertheless, as Fig. 5 indicates, there is only a slight gain in potential economic value
from using the increased resolution model. These results are corroborated by Figs. 1-4,
where the economic value curves for the two controls run very close to each other at 1-day
lead time (Fig. 1), and are practically indistinguishable at 3-day and longer lead times
(Figs. 2-4). In comparison, the ensemble forecasts exhibit considerably higher economic
value (Figs. 1-4). The economic value added by using an ensemble is 5-10 times more
than that resulting from the use of a higher resolution control forecast (Fig. 5). These results
indicate that using the same computational resources, potentially much more economic
benefit can be gained from generating an ensemble of forecasts than from increasing the
horizontal resolution of the control forecast.
5. Conclusions
One can draw the following conclusion from the above results. At and beyond 3 days
lead time, the direct model output from the ensemble forecasts offers more economic
value, and for a wider range of users, than that from control forecasts. For a wide range of
users this also holds true for shorter lead times. These findings confirm earlier results by
ECMWF (Richardson, 2000a) and UK Met. Office (Mylne, 1999) scientists. Using roughly
the same resources, the introduction of an ensemble of forecasts can bring 5-10 times
more economic gain than an increase in the resolution of the control forecast. Therefore
the use of an ensemble forecast system can significantly increase the overall economic
benefit weather predictions can deliver to society.
6. Discussion
a. Why the ensemble approach is successful
The superior performance of the ensemble forecast system is due to two factors.
First, the ensemble can distinguish between forecasts with higher and lower than average
uncertainty at the time the forecasts are issued (Toth et al., 2000). As Toth et al. (1998)
showed by using ROC, Brier score, Ranked Probability Skill Score, and information content
as measures of forecast performance, the ensemble provides important extra information
to the users through its case dependent reliability estimates.
The ensemble technique's second advantage is that it generates probabilistic
forecasts with a multitude of probability values, as compared to dichotomous probability
values provided by a single control forecast1. This again, as Toth et al. (1998) showed by
using different probabilistic verification measures, makes a significant difference.
Multiple-value probability forecasts can of course be constructed based on a single
deterministic forecast, using past verification statistics. Such a system produces
statistically postprocessed, bias-free probabilistic forecasts. Nevertheless, this system
was still found deficient by Talagrand and Candille (1999, personal communication) when
compared to the performance of statistically not postprocessed ensemble forecast
systems. The ensemble's superior performance in their comparison, since the control
forecast was also expressed in the form of a full probability distribution, can only be due to
its ability to do well capturing day-to-day variations in the expected reliability of the
forecasts.
There is a third aspect in which the control and ensemble forecasts differ, and that is
their overall accuracy, measured, e. g., by the hit rate of the control vs. ensemble mode
forecast. At short lead times, the control has an advantage due to its higher resolution (see,
e. g., Fig. 3 of Toth et al., 1998), while at longer lead times the ensemble has an advantage,
due to its nonlinear error filtering capability (Toth and Kalnay, 1997). While these
differences may be significant, comparing Figs. 3 and 7 of Toth et al. (1998) suggests that
they play a secondary role compared to the influence of flow dependent full probability
distributions, discussed above.
b. Limitations, and possible generalization of results
All the results presented in this study pertain to forecasts of the 500 hPa height over
the Northern Hemisphere extratropics, considered as one of the most predictable
atmospheric variables. Comparing Figs. 1-4 it is evident that the more uncertainty (at
longer lead times) a forecast has, the more value the ensemble approach has compared to
using a higher horizontal resolution control only. Even for this highly predictable variable,
beyond 3 days lead time the ensemble system appears to be sufficient (Ehrendorfer and
Murphy, 1988) for the high resolution control forecast, i. e., the traditionally produced high
resolution control forecast has no value for any user when compared to the lower resolution
ensemble.
Based on the 500 hPa results presented in this study one could make a case that,
because the lower resolution ensemble is sufficient for the high resolution control forecast,
and it can be generated at a comparable cost, there is no need for generating a higher
resolution control forecast beyond 3 days. Due to a higher level of uncertainty, variables
other than the 500 hPa height, related more closely to sensible weather, are expected to
benefit more from the ensemble approach. One can hypothesize that in the presence of
any forecast uncertainty, ensemble forecasts may have value for some users; and if the
forecasts exhibit substantial uncertainty (which is at or beyond 3 days lead time for NH
extratropical height forecasts) it is sufficient to run ensemble forecasts only.
Ensemble forecasts for sensible weather elements should preferably be statistically
postprocessed to eliminate possible systematic errors or model biases to facilitate their
general use in weather forecasting. Statistical postprocessing has also been a critical
element in the interpretation of traditional single control forecasts (e. g., Carter et al., 1989).
Note that the purpose of statistical postprocessing of the ensemble forecasts is different
from that of a single control forecast. MOS, for example, not only attempts to eliminate the
bias from the forecasts on which it is applied but also hedges the forecasts (Murphy, 1978)
toward climatology (the larger the expected forecast error, the more so). A single control
forecast is normally used to provide a best estimate of the future state of the atmopshere,
and hedging serves well this purpose. Ensemble forecasting, however, has a different goal,
providing a full forecast probability distribution. In this case hedging, that brings all
forecasts, intended to represent the inherent forecast uncertainty, closer to climatology is
counterproductive .
.
c. Implications for weather forecasting
The role of forecasters is to provide all relevant information on future weather to the
users. The users in turn can take this information, along with other factors, into
consideration when making their decisions related to operations that are sensitive to the
weather (Pielke, 1999). As the results and discussion above indicate, it is critical that the
users have access to multiple-value probabilistic information that capture the large
day-to-day variations in the expected reliability of the forecasts. Such information
facilitates the use, and increases the potential economic value of weather forecasts. It is
not surprising that companies selling weather derivatives3 are among the core users of
ensemble forecasts.
A weather forecast is in fact not complete unless it is expressed in the form of full and
joint probability distributions. And in the case of appreciable uncertainty, the goal of
weather forecasting, including statistical postprocessing, such as MOS and other
methods, should not be the provision of a best estimate of the state of the atmosphere but
rather of a full probability distribution (Murphy, 1977). Given considerable forecast
uncertainty, users with all cost-loss ratios can benefit more from the use of an ensemble of
forecasts than from a single, even higher resolution forecast.
As we saw in Figs. 1-4 the range of users who can derive economic benefit from
using a traditional control forecast compared to climatology is relatively narrow. It is also
clear from the figures that access to ensemble guidance makes weather forecasts useful
for a wide range of additional users. Many of these users who could potentially benefit from
ensemble forecasts may be unaware of this, because of their possible negative experience
with weather guidance that was based on a single control forecast. They may not realize,
until they are introduced to probabilistic forecasting, that the relatively low average hit rate
of certain weather forecasts is not an obstacle to their usage, given the forecast
probabilities show variations from case to case. This may be especially true for users with
high or low cost-loss ratios.
Initially, some users may feel uncomfortable with the notion of "probababilities",
thinking they need to make decisions and for that they need a "yes or no" forecast. The idea
behind the cost-loss analysis discussed above is that if reliable probabilistic forecasts are
available, each user can choose, depending on their estimated or known cost-loss ratio, a
different criterion (probability level) for making their own "yes-no" decision. After all,
weather forecasters are for making weather forecasts, and decision makers are for making
decisions (Murphy, 1978). If the forecaster conveys all available information, the weather
forecast, for example, will be no longer "yes, it will rain", but rather, "there is an 80% chance
of rain". Users with cost-loss ratios 0.8 and below will interpret this forecast as "yes", while
those with ratios above 0.8 as "no". We know that each weather forecast has an associated
uncertainty, and that this unceratinty can generally be quantified by an ensemble of
forecasts; it is in the users' best interest to seek and utilize this information.
d. An example
As an example, let us consider the use of minimum temperature forecasts by two
farmers in the same geographical area who grow different crops that are all sensitive to
freezing temperature. Let us assume that the cost of protecting their crops is the same but
their potential loss differs dramatically due to differences in the vulnerability and value of
their crops. The farmer with less to lose (C/La=0.9, high cost-loss ratio) will only spend on
protection if the frost is almost a certainty (p=0.9, or higher forecast probabilities), whereas
the farmer who can suffer large losses (C/La=0.05) will want to take protective action even if
the forecast probability values are low (p=0.05, or higher). Note that in this example the
farmers translate the probabilistic weather forecast into their "protect - do not protect",
yes-no decision, using very different decision criteria (low vs. high probability values).
If a forecaster provides only his/her best estimate on whether the minimum
temperature will be above or below freezing, this forecast will likely be useless for either
farmer (cf. Fig. 2). Such a forecast, with an intermediate average hit rate of say 60%, will be
useful only for users with intermediate cost-loss ratios. Neither the low, nor the high
cost-loss ratio customer can benefit from such a product. Instead, they will use
climatological information and the former farmer will always, while the latter never protect
his/her crop. To be of any use for them, the forecasts would need to be issued in the form of
multiple probability values; and as we saw such guidance can be readily derived from an
ensemble of forecasts. Such guidance can lead to substantial savings for the farmer with
low (high) cost-loss ratio by identifying cases when he/she can forgo protecting
(implement protection).
7. Acknowledgements
The authors are indebted to David Richardson of ECMWF, and Ken Mylne of the UK
Met. Office who provided advice, and detailed comments on an earlier version of the
manuscript. The comments of Roger Pielke of NCAR, Anthony Barnston and Peter Caplan
of NCEP, and John Jacobson of GSC were also helpful. We acknowledge the support and
encouragement of Stephen Lord, Director of EMC.
8. References
Carter, G. M., J. P. Dallavalle, and H. R. Glahn, 1989: Statistical forecasts based on the
National Meteorological Center's numerical weather prediction system. Wea. Forecasting, 4, 401-412.
Ehrendorfer, M., and A. H. Murphy, 1988: Comparative evaluation of weather forecasting
systems: Sufficiency, quality and accuracy. Mon. Wea. Rev., 116, 1757-1770.
Houtekamer, P. L., and J. Derome, 1995: Methods for ensemble prediction. Mon. Wea.
Rev., 123, 2181-2196.
Houtekamer, P. L., L. Lefaivre, J. Derome, H. Ritchie, and H. L. Mitchell, 1996: A system
simulation approach to ensemble prediction. Mon. Wea. Rev., Mon. Wea. Rev., 124,
1225-1242.
Katz, R. W., and A. H. Murphy, 1997: Economic value of weather and climate forecasts.
Eds., Cambridge University Press, 222 pp.
C. Kobayashi, C., K. Yoshimatsu, S. Maeda, and K. Takano, 1996: Dynamical one-month
forecasting at JMA. Preprints of the 11th AMS Conference on Numerical Weather Prediction, Aug. 19-23, 1996, Norfolk, Virginia, 13-14.
Leith, C. E., 1974: Theoretical skill of Monte Carlo forecasts. Mon. Wea. Rev., 102,
409-418.
Mason, I. B., 1982: A model for the assessment of weather forecasts. Australian Meteorological Magazine, 30, 291-303.
Molteni, F., R. Buizza, T. N. Palmer, and T. Petroliagis, 1996: The ECMWF ensemble system: Methodology and validation. Q. J. R. Meteorol. Soc., 122, 73-119.
Murphy, A. H., 1966: A note on the utility of probabilistic predictions and the probability
score in the cost-loss ratio decision situation. J. Appl. Meteor., 5, 534-537.
Murphy, A. H., 1977: The value of climatological, categorical and probabilistic forecasts in
the cost-loss ratio situation. Mon. Wea. Rev., 105, 803-816.
Murphy, A. H., 1978: Hedging and the mode of expression of weather forecasts. Bull. Amer.
Meteorol. Soc., 59, 371-373.
Murphy, A. H., 1985: Decision making and the value of forecasts in a generalized model
of the cost-loss ratio situation. Mon. Wea. Rev., 113, 362-369.
Murphy, A. H., 1986: Comparative evaluation of categorical and probabilistic forecasts:
Two alternatives to the traditional approach. Mon. Wea. Rev., 114, 245-249.
Mylne, K.R., 1999 The use of forecast value calculations for optimal decision making using
probability forecasts. Preprints of the 17th AMS Conference on Weather Analysis and
Forecasting, 13-17 September 1999, Denver, Colorado, 235-239.
Pielke, Jr., R. A., 1999: Who Decides? Forecasts and Responsibilities in the 1997 Red
River Floods. Applied Behavioral Science Review, 7, 83-101.
Rennick, M. A., 1995: The ensemble forecast system (EFS). Models Department Technical
Note 2-95, Fleet Numerical Meteorology and Oceanography Center. p. 19. [Available
from: Models Department, FLENUMMETOCCEN, 7 Grace Hopper Ave.,Monterey, CA
93943.]
Richardson, D. S., 2000a: Skill and economic value of the ECMWF ensemble prediction
system, Q.J.R.Meteorol. Soc., 126, 649-668.
Richardson, D. S., 2000b: The application of cost-loss models to forecast verification. Proceedings of the Seventh ECMWF Workshop on Meteorological Operational Systems.
November 15-19, 1999, Reading, England, in print.
Stanski, H. R., L. J. Wilson, and W. R. Burrows, 1989: Survey of common verification methods in meteorology. WMO World Weather Watch Technical Report No. 8, WMO/TD. No.
358.
Stuart, T. R., 1997: Forecast value: descriptive decision studies. In: Economic value of
weather and climate forecasts. Ed. by R. W. Katz and A. H. Murphy, Cambridge University Press, 147-181.
Talagrand, O., R. Vautard, and B. Strauss, 1998: Evaluation of probabilistic prediction
systems. Proceedings of ECMWF Workshop on Predictability, 20-22 October 1997,
1-25.
Toth, Z., and E. Kalnay, 1997: Ensemble forecasting at NCEP and the breeding method.
Mon. Wea. Rev, 125, 3297-3319.
Toth, Z., Y. Zhu, T. Marchok, S. Tracton, and E. Kalnay, 1998: Verification of the NCEP global ensemble forecasts. Preprints of the 12th Conference on Numerical Weather Prediction, 11-16 January 1998, Phoenix, Arizona, 286-289.
Toth, Z., Y. Zhu, and T. Marchok, 2000: On the ability of ensembles to distinguish between
forecasts with small and large uncertainty. Proceedings of the Seventh ECMWF Workshop on Meteorological Operational Systems. November 15-19, 1999, Reading, England, in print.
Zhu, Y, G. lyengar, Z. Toth, M. S. Tracton, and T. Marchok, 1996: Objective evaluation of
the NCEP global ensemble forecasting system. Preprints of the 15th AMS Conference
on Weather Analysis and Forecasting, 19-23 August 1996, Norfolk, Virginia, p.
J79-J82.
1#. The yes-no forecast of a deterministic system, based on past verification statistics, can be
converted to dichotomous probabilistic forecasts just as the ensemble-based probabilistic
forecasts can be calibrated, see, e. g., Murphy, 1986, and Toth et al., 1998.
3#. Weather derivatives are insurance policies offered for premiums that depend on expected forecast reliability. The insured receives a payment in case a weather forecast fails.
 . In a case where the event
is not forecast the user does not take action, and if the event does not occur (correct
rejection, CR), there is no cost (N) on the part of the user. If an event is not forecast but
occurs (missed event, M), the user is not protected and suffers a loss (L>C). When,
following the forecast of a harmful event a user takes protective action and the event occurs
(hit, H), the user has to pay the cost of his action (C), plus may still incur some reduced loss,
with a total cost called mitigated loss (ML; typically, C<ML<L).
. In a case where the event
is not forecast the user does not take action, and if the event does not occur (correct
rejection, CR), there is no cost (N) on the part of the user. If an event is not forecast but
occurs (missed event, M), the user is not protected and suffers a loss (L>C). When,
following the forecast of a harmful event a user takes protective action and the event occurs
(hit, H), the user has to pay the cost of his action (C), plus may still incur some reduced loss,
with a total cost called mitigated loss (ML; typically, C<ML<L).

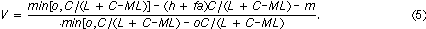
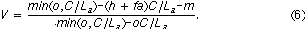
 we show the economic value of the two control forecasts vs. an ensemble of
forecasts at 24-hour lead time, as a function of the La/C ratio, as discussed above. The
economic value comparison results indicate that even at this short, 24-hour lead time, for
this well predictable variable, most potential users, except those with loss-cost ratios in a
relatively narrow band between 2 and 5, can realize more economic value when using the
ensemble forecasts. At and beyond 72 hours lead time (Figs. 2-4)
we show the economic value of the two control forecasts vs. an ensemble of
forecasts at 24-hour lead time, as a function of the La/C ratio, as discussed above. The
economic value comparison results indicate that even at this short, 24-hour lead time, for
this well predictable variable, most potential users, except those with loss-cost ratios in a
relatively narrow band between 2 and 5, can realize more economic value when using the
ensemble forecasts. At and beyond 72 hours lead time (Figs. 2-4)

 virtually all users are
better off using the ensemble system than the control forecasts. Furthermore, the range of
loss-cost ratios for which the forecasts exhibit value, compared to using climatological
information only, is substantially widened, indicating that a much larger group of users can
benefit from the ensemble forecasts as compared to the control forecasts. Note that on
each of the figures the largest economic benefit is, as expected theoretically (see, e. g.,
Richardson, 2000a), attained by users whose C/La ratio is approximately equal to o, the
climatological frequency of the weather event, which in our case is 0.1. Note also that with
increasing lead time the economic value, as compared to using perfect forecasts, just as
the forecast information content (see Fig. 8 of Toth et al., 1998), is reduced.
virtually all users are
better off using the ensemble system than the control forecasts. Furthermore, the range of
loss-cost ratios for which the forecasts exhibit value, compared to using climatological
information only, is substantially widened, indicating that a much larger group of users can
benefit from the ensemble forecasts as compared to the control forecasts. Note that on
each of the figures the largest economic benefit is, as expected theoretically (see, e. g.,
Richardson, 2000a), attained by users whose C/La ratio is approximately equal to o, the
climatological frequency of the weather event, which in our case is 0.1. Note also that with
increasing lead time the economic value, as compared to using perfect forecasts, just as
the forecast information content (see Fig. 8 of Toth et al., 1998), is reduced.
 we show the ROC-area scores for the T62 and
T126 control, and the T62 ensemble forecast systems, for different lead times. Recall that
the ROC-area can be considered as a summary measure of overall economic value of the
forecasts (Richardson, 2000b). The exact implicit assumption in the ROC-area
calculations about the distribution of value protected by different users with respect to their
cost-loss ratio is not known. Unfortunately, little if any information is available on most
users' cost-loss ratio either. Nevertheless Fig. 5 can provide an indication for the overall
utility of the three forecast systems. Perfect (climatological) forecasts correspond to a
value of 0.5 (0) ROC area, while negative values indicate economic loss compared to using
climatological guidance.
we show the ROC-area scores for the T62 and
T126 control, and the T62 ensemble forecast systems, for different lead times. Recall that
the ROC-area can be considered as a summary measure of overall economic value of the
forecasts (Richardson, 2000b). The exact implicit assumption in the ROC-area
calculations about the distribution of value protected by different users with respect to their
cost-loss ratio is not known. Unfortunately, little if any information is available on most
users' cost-loss ratio either. Nevertheless Fig. 5 can provide an indication for the overall
utility of the three forecast systems. Perfect (climatological) forecasts correspond to a
value of 0.5 (0) ROC area, while negative values indicate economic loss compared to using
climatological guidance.
 .
.